
题目列表(包括答案和解析)
 如图,某数学课外活动小组测量电视塔AB的高度.他们借助一个高度为30m的建筑物CD进行测量,在点C处测得塔顶B的仰角为45°,在点E处测得B的仰角为37°(B、D、E三点在一条直线上).求电视塔的高度h.
如图,某数学课外活动小组测量电视塔AB的高度.他们借助一个高度为30m的建筑物CD进行测量,在点C处测得塔顶B的仰角为45°,在点E处测得B的仰角为37°(B、D、E三点在一条直线上).求电视塔的高度h.如图,某数学课外活动小组测量电视塔AB的高度,他们借助一个高度为30m的建筑物CD进行测量,在点C处塔顶B的仰角为45°,在点E处测得B的仰角为37°(B、D、E三点在一条直线上).求电视塔的高度h.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

(2011•南京)如图,某数学课外活动小组测量电视塔AB的高度.他们借助一个高度为30m的建筑物CD进行测量,在点C处测得塔顶B的仰角为45°,在点E处测得B的仰角为37°(B、D、E三点在一条直线上).求电视塔的高度h.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)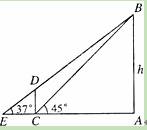

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com