练习册

  • 练习册
  • 试题
    证: ⑴∵AD∥BC ∴AD∥CE 又∵DE∥AC ∴四边形ACED是平行四边形------ 4分 ⑵过D点作DF⊥BE于F点 --------5分 ∵DE∥AC.AC⊥BD ∴DE⊥BD.即∠BDE=90°--------6分 由⑴知DE=AC.CE=AD=3 ∵四边形ABCD是等腰梯形 ∴AC=DB----7分 ∴DE=DB ------------8分 ∴△DBE是等腰直角三角形.∴△DFB也是等腰直角三角形 ∴DF=BF=(7-3)+3=5--------10分 (也可运用:直角三角形斜边上的中线等于斜边的一半“) --12分 注:⑴过对角线交点O作OF⊥BC于F.延长FO交AD于H.于是OH⊥AD 由△ABC≌△DCB.得到△OBC是等腰直角三角形.OF=BC= 同理OH=AD=.高HF= ⑵过A作AF⊥BC于F.过D作DH⊥BC于H.由△AFC≌△DHB 得高AF=FC==5 ⑶ 【查看更多】

     

    题目列表(包括答案和解析)

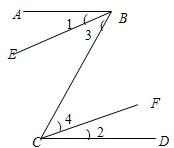    10、如图所示，已知∠1=∠2，若要证∠3=∠4，则需要（　　）

    查看答案和解析>>

    如图所示，已知∠1=∠2，若要证∠3=∠4，则需要（　　）
    A．∠1=∠3B．∠2=∠3C．AB∥CDD．∠1=∠4
    精英家教网

    查看答案和解析>>

    (创新题)“有两边相等的两个直角三角形全等”这个命题对与否，甲、乙、丙三位同学给出了如下论断：

    　　甲：正确．因为若两边都是直角边，则用(S.A.S.)全等识别法就可以证它们全等．

    　　乙：正确．因为若其中一边是直角边，另一边是斜边，则可用(H.　L.)定理证全等．

    　　丙：不正确．若一个三角形较长的直角边与另一三角形斜边相等，较短的直角边与另一三角形较长的直角边相等，则显而易见两个三角形不全等．

    请你就这三个同学的见解发表自己的意见．

    查看答案和解析>>

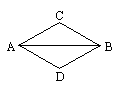
    如图所示，若AB平分∠DAC，要用SAS公理证△ABC≌△ABD，需再有条件

    [　　]

    A．DB＝CB
    B．AB＝AB
    C．AD＝AC
    D．∠D＝∠C

    查看答案和解析>>

    我们知道，两边及其中一边的对角分别对应相等的两个三角形不一定全等．那么在什么情况下，它们会全等

    　　(1)阅读与证明：

    　　对于这两个三角形均为直角三角形，显然它们全等．

    　　对于这两个三角形均为钝角三角形，可证它们全等(证明略)．

    　　对于这两个三角形均为锐角三角形，它们也全等，可证明如下：

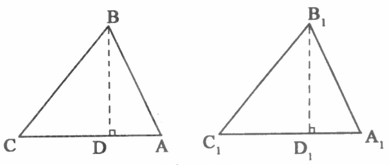
    　　已知：△ABC、△A1B1C1均为锐角三角形，AB=A1B1，BC=B1Cl，∠C=∠Cl．

    　　求证：△ABC≌△A1B1C1．

    (请你将下列证明过程补充完整．)

    证明：分别过点B，B1作BD⊥CA于D，B1 D1⊥C1 A1于D1.

    　　则∠BDC=∠B1D1C1=900，

    　　∵BC=B1C1，∠C=∠C1，

    　　∴△BCD≌△B1C1D1，-

    　　∴BD=B1D1．

    (2)归纳与叙述：

    由(1)可得到一个正确结论，请你写出这个结论．

    查看答案和解析>>


    同步练习册答案