
题目列表(包括答案和解析)
(本题满分14分)
如图是某市一条河上一座古拱挢的截面图,拱桥桥洞上沿是抛物线形状,抛物线拱桥处于正常水位时水面宽AB为26m,当水位上涨1m时,抛物线拱桥的水面宽CD为24m.现以水面AB所在直线为x轴,抛物线的对称轴为y轴建立直角坐标系.
【小题1】(1) 求出抛物线的解析式;
【小题2】(2) 经过测算,水面离拱桥顶端1.5m时为警戒水位.某次洪水到来时,小明用仪器测得水面宽为10m,请你帮助小明算一算,此时水面是否超过警戒水位.
(本题满分14分)
如图是某市一条河上一座古拱挢的截面图,拱桥桥洞上沿是抛物线形状,抛物线拱桥处于正常水位时水面宽AB为26m,当水位上涨1m时,抛物线拱桥的水面宽CD为24m.现以水面AB所在直线为x轴,抛物线的对称轴为y轴建立直角坐标系.

1.(1) 求出抛物线的解析式;
2.(2) 经过测算,水面离拱桥顶端1.5m时为警戒水位.某次洪水到来时,小明用仪器测得水面宽为10m,请你帮助小明算一算,此时水面是否超过警戒水位.
(本题满分14分)
如图是某市一条河上一座古拱挢的截面图,拱桥桥洞上沿是抛物线形状,抛物线拱桥处于正常水位时水面宽AB为26m,当水位上涨1m时,抛物线拱桥的水面宽CD为24m.现以水面AB所在直线为x轴,抛物线的对称轴为y轴建立直角坐标系.
1.(1) 求出抛物线的解析式;
2.(2) 经过测算,水面离拱桥顶端1.5m时为警戒水位.某次洪水到来时,小明用仪器测得水面宽为10m,请你帮助小明算一算,此时水面是否超过警戒水位.
.(本题满分12分) 如图,在平面直角坐标系中,四边形OABC为直角梯形,OA∥BC,BC=14,A(16,0),C(0,2).
1.(1)如图①,若点P、Q分别从点C、A同时出发,点P以每秒2个单位的速度由C向B运动,点Q以每秒4个单位的速度由A向O运动,当点Q停止运动时,点P也停止运动.设运动时间为t秒(0≤t≤4).
①求当t为多少时,四边形PQAB为平行四边形?(4分)
②求当t为多少时,直线PQ将梯形OABC分成左右两部分的比为1:2,并求出此时直线PQ的解析式. (4分)
2.(2)如图②,若点P、Q分别是线段BC、AO上的任意两点(不与线段BC、AO的端点重合),且四边形OQPC面积为10,试说明直线PQ一定经过一定点,并求出该定点的坐标. (4分)
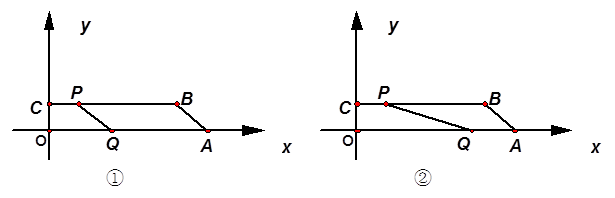
.(本题满分12分) 如图,在平面直角坐标系中,四边形OABC为直角梯形,OA∥BC,BC=14,A(16,0),C(0,2).
1.(1)如图①,若点P、Q分别从点C、A同时出发,点P以每秒2个单位的速度由C向B运动,点Q以每秒4个单位的速度由A向O运动,当点Q停止运动时,点P也停止运动.设运动时间为t秒(0≤t≤4).
①求当t为多少时,四边形PQAB为平行四边形?(4分)
②求当t为多少时,直线PQ将梯形OABC分成左右两部分的比为1:2,并求出此时直线PQ的解析式. (4分)
2.(2)如图②,若点P、Q分别是线段BC、AO上的任意两点(不与线段BC、AO的端点重合),且四边形OQPC面积为10,试说明直线PQ一定经过一定点,并求出该定点的坐标. (4分)

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com