
题目列表(包括答案和解析)
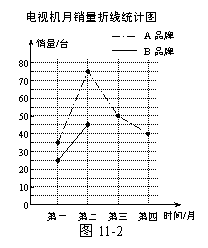
某商店在四个月的试销期内,只销售A、B两个品牌的电视机,共售出400台.试销结束后,只能经销其中的一个品牌,为作出决定,经销人员正在绘制两幅统计图,如图11-1和图11-2.
电视机月销量扇形统计图 |
| 第一个月 15% |
| 第二个月 30% |
| 第三个月 25% |
| 第四个月 |
图11-1 |
(1)第四个月销量占总销量的百分比是
(2)在图11-2中补全表示B品牌电视机月销量的
折线;
(3)为跟踪调查电视机的使用情况,从该商店第
四个月售出的电视机中,随机抽取一台,求
抽到B品牌电视机的概率;
(4)经计算,两个品牌电视机月销量的平均水平相
同,请你结合折线的走势进行简要分析,判断
该商店应经销哪个品牌的电视机.
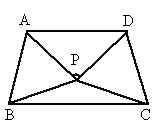
如图,△ABP和△DCP是两个全等的等边三角形,且PA⊥PD,有下列四个结论:(1)∠PBC=15°;(2)AD∥BC;(3)直线PC与AB垂直;(4)四边形ABCD是轴对称图形.其中正确结论的个数为
[ ]
如图,△ABP和△DCP是两个全等的等边三角形,且PA⊥PD,有下列四个结论:(1)∠PBC=15°;(2)AD∥BC;(3)直线PC与AB垂直;(4)四边形ABCD是轴对称图形.其中正确结论的个数为
[ ]
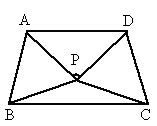
(2004 重庆)如图所示,在圆O的内接△ABC中,AB=AC,D是圆O上一点,AD的延长线交BC的延长线于点P.
(1)求证: ;
;
(2)若圆O的直径为25,AB=20,AD=15,求PC和DC的长.
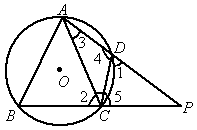
 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交 CE于点G,连接BE.下列结论中:
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交 CE于点G,连接BE.下列结论中:湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com