掷一枚质量均匀的正六面体的骰子200次，记录如下(为便于统计，每5次列为1组)：

44551　33243　12654　23541　16613　42565　11654　31522　36436　1652

23455　12346　13216　63226　14553　26533　23456　65511　66412　44215

51364　23123　65414　65623　54321　56323　12466　55122　36414　14236

21544　63123　51616　46352　26453　22311　14566　45453　36123　51462

(1)将数据整理后填入表4中．

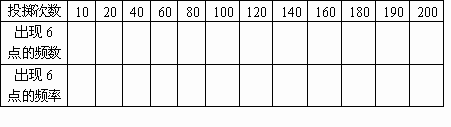
(2)分别计算投掷10次和20次、180次和190次、190次和200次后频率的值的差．你从中发现了什么？比较表1的摸球实验，这两种实验是否有类似之处？

(3)随着实验次数的增加，估计掷得6点的机会约是________．

用实验的方法估计下列事件发生的概率：

(1)掷一枚均匀的硬币，反面朝上；

(2)掷一枚均匀的骰子，点数为5；

(3)掷一枚均匀的骰子，每次实验掷两枚，两次骰子的点数和为5．

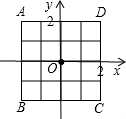如图，放在直角坐标系中的正方形ABCD边长为4，现做如下实验：抛掷一枚均匀的正四面体骰子（它有四个顶点，各顶点的点数分别是1至4这四个数字中一个），每个顶点朝上的机会是相同的，连续抛掷两次，将骰子朝上的顶点数作为直角坐标中P点的坐标）第一次的点数作横坐标，第二次的点数作纵坐标）．
（1）求P点落在正方形ABCD面上（含正方形内部和边界）的概率．
（2）将正方形ABCD平移整数个单位，则是否存在一种平移，使点P落在正方形ABCD
面上的概率为

3

4

；若存在，指出其中的一种平移方式；若不存在，请说明理由．

随机掷一枚均匀的正方体骰子（正方体骰子的六个面上的点数分别为1，2，3，4，5，6），每次实验掷两次，则每次实验中掷两次骰子的点数之和为6的概率是．