
题目列表(包括答案和解析)
(本题满分12分)
如图所示,在平面直角坐标系中,顶点为(![]() ,
,![]() )的抛物线交
)的抛物线交![]() 轴于
轴于![]() 点,交
点,交![]() 轴于
轴于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),已知
的左侧),已知![]() 点坐标为(
点坐标为(![]() ,
,![]() ).
).

(1)求此抛物线的解析式;
(2)过点![]() 作线段
作线段![]() 的垂线交抛物线于点
的垂线交抛物线于点![]() ,
,
如果以点![]() 为圆心的圆与直线
为圆心的圆与直线![]() 相切,请判断抛物
相切,请判断抛物
线的对称轴![]() 与⊙
与⊙![]() 有怎样的位置关系,并给出证明;
有怎样的位置关系,并给出证明;
(3)已知点![]() 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于![]() ,
,
![]() 两点之间,问:当点
两点之间,问:当点![]() 运动到什么位置时,
运动到什么位置时,![]() 的
的
面积最大?并求出此时![]() 点的坐标和
点的坐标和![]() 的最大面积.
的最大面积.
(本题满分12分)我们设想用电脑模拟台球游戏,为简单起见,约定:①每个球袋视为一个点,如果不遇到障碍,各球均沿直线前进;②A球击B球,意味着B球在A球前进的路线上,且B球被撞击后沿A球原来的方向前进;③球撞击桌边后的反弹角度等于入射角度,(如图中∠β=∠a)如图所示,设桌边只剩下白球,A,6号球B。
(1)希望A球撞击桌边上C点后反弹,再击中B球,请给出一个算法,告知电脑怎样找到点C,并求出C点的坐标。
(2)设桌边RQ上有一球袋S(100,120),判定6号球B被从C点反弹出的白球撞击后能否直接落入球袋S中,(假定6号球被撞后速度足够大)。
(3)若用白球A直接击打6号球B,使6号球B撞击桌边OP上的D点后反弹,问6号球B从D点反弹后能否直接进入球袋Q中?(假定6号球被撞后速度足够大)
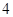 ,
,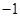 )的抛物线交
)的抛物线交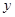 轴于
轴于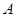 点,交
点,交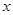 轴于
轴于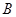 ,
,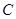 两点(点
两点(点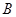 在点
在点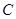 的左侧), 已知
的左侧), 已知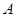 点坐标为(
点坐标为( ,
,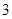 ).
).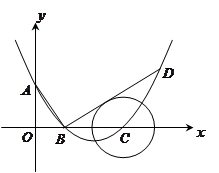
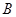 作线段
作线段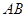 的垂线交抛物线于点
的垂线交抛物线于点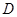 ,
,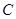 为圆心的圆与直线
为圆心的圆与直线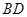 相切,请判断抛物
相切,请判断抛物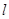 与⊙
与⊙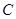 有怎样的位置关系,并给出证明;
有怎样的位置关系,并给出证明;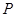 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于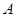 ,
,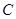 两点之间,问:当点
两点之间,问:当点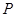 运动到什么位置时,
运动到什么位置时,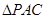 的
的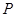 点的坐标和
点的坐标和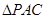 的最大面积.
的最大面积.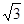 ,矩形ABOC绕点O按顺时针方向旋转60°后得矩形EFOD. 点A的对应点为点E,点B的对应点为F,点C的对应点为点D. 抛物线
,矩形ABOC绕点O按顺时针方向旋转60°后得矩形EFOD. 点A的对应点为点E,点B的对应点为F,点C的对应点为点D. 抛物线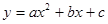 过点A、E、D.
过点A、E、D.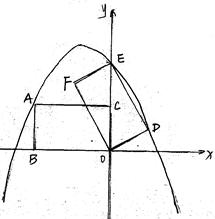

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com