
题目列表(包括答案和解析)
| 2 |
| 3 |
| m2n |
| 2 |
| 1 |
| x |
| 2 |
| y |
| 3 |
| ab |
| m-n |
| m+n |
| x-1 |
| 2 |
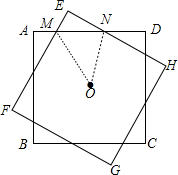 在一次研究性学习活动中,某小组将两张互相重合的正方形纸片ABCD和EFGH的中心O用图钉固定住,保持正方形ABCD不动,顺时针旋转正方形EFGH,如图所示.
在一次研究性学习活动中,某小组将两张互相重合的正方形纸片ABCD和EFGH的中心O用图钉固定住,保持正方形ABCD不动,顺时针旋转正方形EFGH,如图所示.| 1 |
| 2 |
| 3 | -64 |
| •• |
| 32 |
| 5 |
| 16 |
| π |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com