
题目列表(包括答案和解析)
如图A表示三经路与一纬路的十字路口,B表示一经路与三纬路的十字路口,如果用(3,1)→(3,2)→(3,3)→(2,3)→(1,3)表示由A到B的一条路径,用同样的方式写出另一条由A到B的路径:(3,1)→______→______→______→______(1,3).
如图表示一艘轮船与一艘快艇沿相同路线从甲港到乙港行驶过程中路程随时间变化的图象(分别是正比例函数图象和一次函数图象).根据图象解答下列问题:

(1)快艇比轮船晚出发________时,早到________时;
(2)轮船在途中(不包括起点和终点)行驶的速度是________1km/h;快艇在途中(不包括起点和终点)行驶的速度是________km/h;
(3)请求出表示轮船行驶过程的函数解析式:________;表示快艇行驶过程的函数解析式:________;
(不要求写出自变量的取值范围)
(4)问快艇出发多长时间赶上轮船?
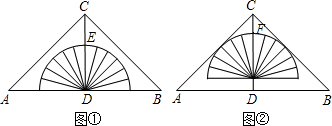 ②.则AB的边长为
②.则AB的边长为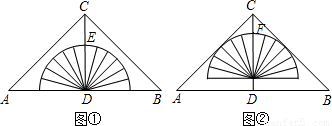
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com