
题目列表(包括答案和解析)
(本小题满分14分)如图,已知矩形ABCD的边AB="2" ,BC= ,点E、F分别是边AB、CD的中点,沿AF、EC分别把三角形ADF和三角形EBC折起,使得点D和点B重合,记重合后的位置为点P。
,点E、F分别是边AB、CD的中点,沿AF、EC分别把三角形ADF和三角形EBC折起,使得点D和点B重合,记重合后的位置为点P。
(1)求证:平面PCE 平面PCF;
平面PCF;
(2)设M、N分别为棱PA、EC的中点,求直线MN与平面PAE所成角的正弦;
(3)求二面角A-PE-C的大小。

(本小题满分14分)如图,已知矩形ABCD的边AB=2 ,BC=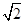 ,点E、F分别是边AB、CD的中点,沿AF、EC分别把三角形ADF和三角形EBC折起,使得点D和点B重合,记重合后的位置为点P。
,点E、F分别是边AB、CD的中点,沿AF、EC分别把三角形ADF和三角形EBC折起,使得点D和点B重合,记重合后的位置为点P。
(1)求证:平面PCE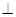 平面PCF;
平面PCF;
(2)设M、N分别为棱PA、EC的中点,求直线MN与平面PAE所成角的正弦;
(3)求二面角A-PE-C的大小。
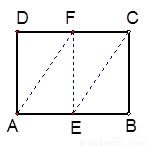
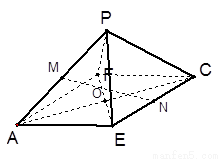
(本小题满分14分)
如图(1)已知矩形 中,
中,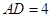 ,
, 、
、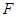 分别是
分别是 、
、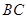 的中点,点
的中点,点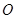 在
在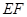 上,且
上,且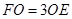 ,把
,把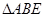 沿着
沿着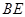 翻折,使点
翻折,使点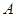 在平面
在平面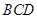 上的射影恰为点
上的射影恰为点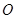 (如图(2))。
(如图(2))。
(1)求证:平面
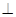 平面
平面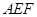 ;
;
(2)求二面角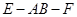 的大小.
的大小.
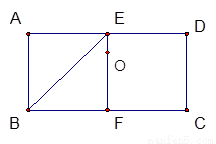
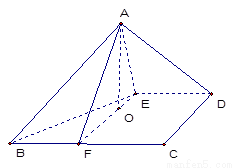
图(1) 图(2)
(本小题满分14分)如图,已知四棱锥 的底面
的底面 是矩形,
是矩形,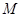 、
、 分别是
分别是 、
、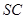 的中点,
的中点,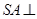 底面
底面 ,
, ,
,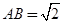
(1)求证: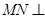 平面
平面
(2)求二面角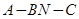 的余弦值
的余弦值

(本小题满分14分)
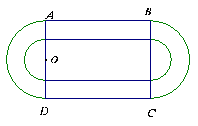 某学校要建造一个面积为10000平方米的运动场.如图,运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元
某学校要建造一个面积为10000平方米的运动场.如图,运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元
(1)设半圆的半径OA=![]() (米),试建立塑胶跑道面积S与
(米),试建立塑胶跑道面积S与![]() 的函数关系S(
的函数关系S(![]() )
)
(2)由于条件限制![]() ,问当
,问当![]() 取何值时,运动场造价最低?(精确到元)
取何值时,运动场造价最低?(精确到元)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com