
题目列表(包括答案和解析)
(本大题10分)(本大题有两题,请同学们选择你喜欢且拿手一题解答)
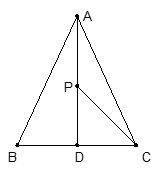
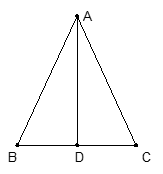
如图,在△ABC中,AB=AC=13厘米,BC=10厘米,AD⊥BC于点D,动点P从点A出发以每秒1厘米的速度在线段AD上向终点D运动。设动点运动时间为t秒。
(1)求AD的长.(3分)
(2)当△PDC的面积为15平方厘米时,求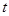 的值.(4分)
的值.(4分)
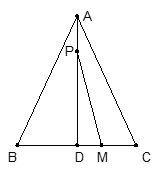
(3)动点M从点C出发以每秒2厘米的速度在射线CB上运动.点M与点P同时出发,且当点P运动到终点D时,点M也停止运动。是否存在t,使得S△PMD=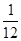 S△ABC?若存在,请求出t的值;若不存在,请说明理由.(5分)
S△ABC?若存在,请求出t的值;若不存在,请说明理由.(5分)



(本大题10分)(本大题有两题,请同学们选择你喜欢且拿手一题解答)
如图,在△ABC中,AB=AC=13厘米,BC=10厘米,AD⊥BC于点D,动点P从点A出发以每秒1厘米的速度在线段AD上向终点D运动。设动点运动时间为t秒。
(1)求AD的长.(3分)
(2)当△PDC的面积为15平方厘米时,求![]() 的值.(4分)
的值.(4分)
(3)动点M从点C出发以每秒2厘米的速度在射线CB上运动.点M与点P同时出发,且当点P运动到终点D时,点M也停止运动。是否存在t,使得S△PMD=![]() S△ABC?若存在,请求出t的值;若不存在,请说明理由.(5分)
S△ABC?若存在,请求出t的值;若不存在,请说明理由.(5分)
(本小题满分10分)
(1)如图24—1,已知△ABC中,∠BAC=45°,AB="AC," AD⊥BC于D, 将△ABC沿AD剪开,并分别以AB、AC为轴翻转,点E、F分别是点D的对应点,得到△ABE和△ACF (与△ABC在同一平面内).延长EB、FC相交于G点,证明四边形AEGF是正方形;
(2)如果⑴中AB≠AC,其他不变,如图24—2.那么四边形AEGF是否是正方形?请说明理由.
(3)在⑵中,若BD=2,DC=3,求AD的长.
(本题10分)如右图,点A是△ABC和△ADE的公共顶点,∠BAC+∠DAE=180°,AB=AE,AC=AD,点M是DE的中点,直线AM交直线BC于点N.将△ADE绕点A旋转,在旋转的过程中,请探究∠ANB与∠BAE的数量关系,并加以证明.
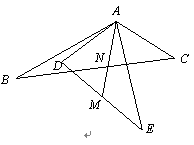
 AE=180°,AB=AE,AC=AD,点M是DE的中点,直线AM交直线BC于点N.将△ADE绕点A旋转,在旋转的过程中,请探究∠ANB与∠BAE的数量关系,并加以证明.
AE=180°,AB=AE,AC=AD,点M是DE的中点,直线AM交直线BC于点N.将△ADE绕点A旋转,在旋转的过程中,请探究∠ANB与∠BAE的数量关系,并加以证明.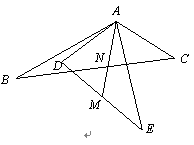
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com