
题目列表(包括答案和解析)
(本小题共14分)
如图,在 中,
中,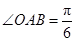 ,斜边
,斜边 .
.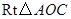 可以通过
可以通过 以直线
以直线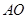 为轴旋转得到,且二面角
为轴旋转得到,且二面角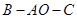 是直二面角.动点
是直二面角.动点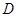 的斜边
的斜边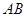 上.
上.
(I)求证:平面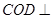 平面
平面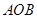 ;
;
(II)当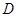 为
为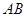 的中点时,求异面直线
的中点时,求异面直线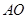 与
与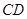 所成角的大小;
所成角的大小;
(III)求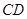 与平面
与平面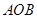 所成角的最大值.
所成角的最大值.
(07年北京卷理)(本小题共14分)
如图,在![]() 中,
中,![]() ,斜边
,斜边![]() .
.![]() 可以通过
可以通过![]() 以直线
以直线![]() 为轴旋转得到,且二面角
为轴旋转得到,且二面角![]() 是直二面角.动点
是直二面角.动点![]() 的斜边
的斜边![]() 上.
上.

(I)求证:平面![]() 平面
平面![]() ;
;
(II)当![]() 为
为![]() 的中点时,求异面直线
的中点时,求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(III)求![]() 与平面
与平面![]() 所成角的最大值.
所成角的最大值.
(本小题共14分)
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD//BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=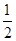 AD=1,CD=
AD=1,CD=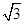 .
.
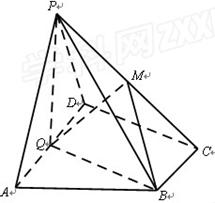
(Ⅰ)若点M是棱PC的中点,求证:PA // 平面BMQ;
(Ⅱ)求证:平面PQB⊥平面PAD;
(Ⅲ)若二面角M-BQ-C为30°,设PM=tMC,试确定t的值 .
(本小题共14分)如图,在三棱锥![]() 中,
中,![]() 底面
底面
![]() ,点
,点![]() ,
,![]() 分别在棱
分别在棱![]() 上,且
上,且![]() (Ⅰ)求证:
(Ⅰ)求证:![]() 平面
平面![]() ;(Ⅱ)当
;(Ⅱ)当![]() 为
为![]() 的中点时,求
的中点时,求![]() 与平面
与平面![]() 所成的角的大小;(Ⅲ)是否存在点
所成的角的大小;(Ⅲ)是否存在点![]() 使得二面角
使得二面角![]() 为直二面角?并说明理由.
为直二面角?并说明理由.
(本小题共14分)如图,四棱锥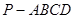 中,底面
中,底面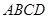 为平行四边形,
为平行四边形,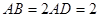 ,
,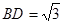 ,
, ⊥底面
⊥底面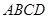 .
.

(1)证明:平面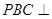 平面
平面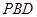 ;
;
(2)若二面角 为
为 ,求
,求 与平面
与平面 所成角的正弦值。
所成角的正弦值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com