
题目列表(包括答案和解析)
【解题思路】通过读题、审题
(1)完成表格有2个思路:从供或需的角度考虑,均能完成上表。
(2)运用公式(调运水的重量×调运的距离)
总调运量=A的总调运量+B的总调运量调运水的重量×调运的距离
y=50x+(14-x)30+60(15-x)+(x-1)45=5x+1275(注:一次函数的最值要得到自变量的取值范围)∵5>0∴y随x的增大而增大,y要最小则x应最大
由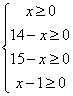 解得1≤x≤14
解得1≤x≤14
y=5x+1275中∵5>0∴y随x的增大而增大,y要最小则x应最小=1
∴调运方案为A往甲调1吨,往乙调13吨;B往甲调14吨,不往乙调。
【答案】⑴(从左至右,从上至下)14-x 15-x x-1
⑵y=50x+(14-x)30+60(15-x)+(x-1)45=5x+1275
解不等式1≤x≤14
所以x=1时y取得最小值
y=5+1275=1280
∴调运方案为A往甲调1吨,往乙调13吨;B往甲调14吨,不往乙调。
| 4 |
| 5 |
| 5 |
| 4 |
| A、方程两边都乘以20,得4(5x-120)=140 | ||||||
B、方程两边都除以
| ||||||
| C、去括号,得x-24=7 | ||||||
D、方程整理,得
|
| 1 | ||
|
| 1 |
| 2 |
| 4 |
| 5 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 4 |
| 2 |
| 3 |
| 4 |
| 5 |
| 9 |
| 10 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com