
题目列表(包括答案和解析)
如图1,在△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长.
小萍同学灵活运用轴对称知识,将图形进行翻折变换如图1.她分别以AB、AC为对称轴,画出△ABD、△ACD的轴对称图形,D点的对称点为E、F,延长EB、FC相交于G点,得到四边形AEGF是正方形.设AD=x,利用勾股定理,建立关于x的方程模型,求出x的值.
(1)请你帮小萍求出x的值.
(2) 参考小萍的思路,探究并解答新问题:
如图2,在△ABC中,∠BAC=30°,AD⊥BC于D,AD=4.请你按照小萍的方法画图,得到四边形AEGF,求△BGC的周长.(画图所用字母与图1中的字母对应)
如图1,在△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长.
小萍同学灵活运用轴对称知识,将图形进行翻折变换如图1.她分别以AB、AC为对称轴,画出△ABD、△ACD的轴对称图形,D点的对称点为E、F,延长EB、FC相交于G点,得到四边形AEGF是正方形.设AD=x,利用勾股定理,建立关于x的方程模型,求出x的值.
(1)请你帮小萍求出x的值.
(2) 参考小萍的思路,探究并解答新问题:
如图2,在△ABC中,∠BAC=30°,AD⊥BC于D,AD=4.请你按照小萍的方法画图,得到四边形AEGF,求△BGC的周长.(画图所用字母与图1中的字母对应)
(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=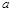 ,其中
,其中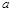 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
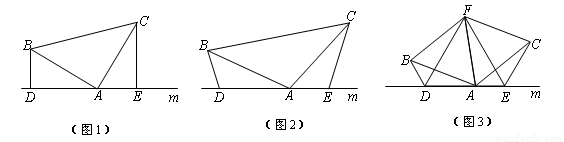
(本题满分10分)如图,在△ABC中,∠BAC=120°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA.
(1)试求∠DAE的度数.
(2)如果把题中“AB=AC”的条件去掉,其余条件不变,那么∠DAE的度数会改变吗?请说明理由. (3)若∠BAC=α°,其它条件与(2)相同,则∠DAE的度数是多少?为什么?
(3)若∠BAC=α°,其它条件与(2)相同,则∠DAE的度数是多少?为什么?
如图,在△ABC中,△BAC=90°,D是BC中点,AE∥AD交CB延长线于点E,则⊿BAE相似于______.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com