（1）请在一个3×2的矩形网格里（每个小正方形的边长都是1），画出一个以格点为顶点的等腰直角三角形，使其直角边长为 $数学公式$ ，并适当加以文字说明．
（2）借助上述图形，解释下列结论：
若α与β为锐角，且tanα= $数学公式$ ，tanβ= $数学公式$ ，则α+β=45°．
（3）构造几何图形，解释下列结论：
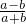若α与β为锐角，且tanα= $数学公式$ ，tanβ= $数学公式$ ，其中a＞b＞0，则α+β=45°．

操作探究：
我们知道一个三角形中有三条高线和三条中线．如图1，AD和AE分别是△ABC中BC边上的高线和中线，我们规定：k_A=

BE′

，另外，对k_B、k_C作类似的规定．
（1）如图2，在△ABC中，∠C=90°，∠A=30°，则k_A的值为

，k_C的值为

；
（2）在每个小正方形边长均为1的4×4的方格纸上（如图3），画一个△ABC，使其顶点在格点（格点即每个小正方形的顶点）上，且k_A=2，面积也为2；
（3）判断下面三个命题的真假（真命题打“√”，假命题的打“×”）
①若△ABC中，k_A＜1，则△ABC为锐角三角形

；
②若△ABC中，k_A=1，则△ABC为直角三角形

√

；
③若△ABC中，k_A＞1，则△ABC为钝角三角形

√

．

阅读以下短文，然后解决下列问题：

如果一个三角形和一个矩形满足条件：三角形的一边与矩形的一边重合，且三角形的这边所对的顶点在矩形这边的对边上，则称这样的矩形为三角形的“友好矩形”．如图(1)所示，矩形ABEF即为△ABC的“友好矩形”．显然，当△ABC是钝角三角形时，其“友好矩形”只有一个．

(1)仿照以上叙述，说明什么是一个三角形的“友好平行四边形”；

(2)如图(2)，若△ABC为直角三角形，且∠C＝90°，在图(2)中画出△ABC的所有“友好矩形”，并比较这些矩形面积的大小；

(3)若△ABC是锐角三角形，且BC＞AC＞AB，在图(3)中画出△ABC的所有“友好矩形”．

阅读下面短文：如图1，△ABC是直角三角形，∠C=90°，现将△ABC补成长方形，使△ABC的两个顶点为长方形一边的两个端点，第三个顶点落在长方形这一边的对边上，那么符合要求的长方形可以画出两个：长方形ACBD和长方形AEFB（如图2）。

解答问题：

（1）设图2中长方形ACBD和长方形AEFB的面积分别为S₁，S₂，则S₁ S₂（填“＞”、“＝”或“＜”）

（2）如图3，△ABC是钝角三角形，按短文中的要求把它补成长方形，那么符合要求的长方形可以画出个，利用图3把它画出来。

（3）如图4，△ABC是锐角三角形且三边满足BC＞AC＞AB，按短文中的要求把它补成长方形，那么符合要求的长方形可以画出个，利用图4把它画出来。

（4）在（3）中所画出的长方形中，哪一个的周长最小？为什么？

如图①，△ABD是直角三角形，∠C＝，现将△ABC补成矩形，使△ABC的两个顶点为矩形一边的两个端点，第三个顶点落在矩形这一边的对边上，则符合要求的矩形可以画出两个：矩形ACBD和矩形AEFB(如图②)．

解答问题：

(1)设图②中矩形ACBD和矩形AEFB的面积分别为S₁，S₂，则S₁_______S₂．(填“＞”、“＝”或“＜”)

(2)如图③，△ABC是钝角三角形，按题设要求把它补成矩形，那么符合要求的矩形可以画出_______个．

(3)如图④，△ABC是锐角三角形，且三边满足BC＞AC＞AB，按题设要求把它补成矩形，那么符合要求的矩形可以画出_______个．

(4)在(3)中所画出的矩形中，哪一个的周长最小？为什么？

同步练习册答案