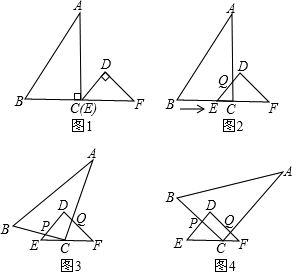
已知:RT△ABC与RT△DEF中,∠ACB=∠EDF=90°,∠DEF=45°,EF=8cm,AC=16cm,BC=12cm.现将RT△ABC和RT△DEF按图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,并按如下方式运动.
运动一:如图2,△ABC从图1的位置出发,以1cm/s的速度沿EF方向向右匀速运动,DE与AC相交于点Q,当点Q与点D重合时暂停运动;
运动二:在运动一的基础上,如图3,RT△ABC绕着点C顺时针旋转,CA与DF交于点Q,CB与DE交于点P,此时点Q在DF上匀速运动,速度为
cm/s,当QC⊥DF时暂停旋转;
运动三:在运动二的基础上,如图4,RT△ABC以1cm/s的速度沿EF向终点F匀速运动,直到点C与点F重合时为止.
设运动时间为t(s),中间的暂停不计时,
解答下列问题
(1)在RT△ABC从运动一到最后运动三结束时,整个过程共耗时
s;
(2)在整个运动过程中,设RT△ABC与RT△DEF的重叠部分的面积为S(cm
2),求S与t之间的函数关系式,并直接写出自变量t的取值范围;
(3)在整个运动过程中,是否存在某一时刻,点Q正好在线段AB的中垂线上,若存在,求出此时t的值;若不存在,请说明理由.

 (2012•济宁)如图,在平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.
(2012•济宁)如图,在平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.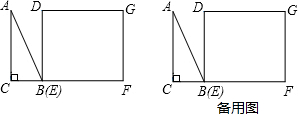 如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°;四边形DEFG为矩形,DE=2
如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°;四边形DEFG为矩形,DE=2 已知:RT△ABC与RT△DEF中,∠ACB=∠EDF=90°,∠DEF=45°,EF=8cm,AC=16cm,BC=12cm.现将RT△ABC和RT△DEF按图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,并按如下方式运动.
已知:RT△ABC与RT△DEF中,∠ACB=∠EDF=90°,∠DEF=45°,EF=8cm,AC=16cm,BC=12cm.现将RT△ABC和RT△DEF按图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,并按如下方式运动.