
题目列表(包括答案和解析)
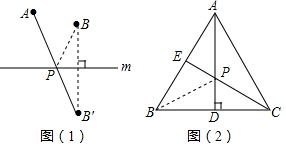
 的度数为60°,点B是
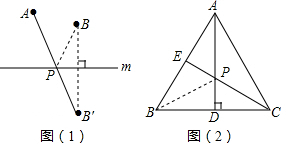
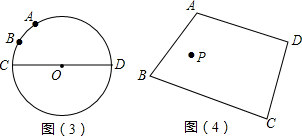
的度数为60°,点B是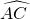 的中点,在直径CD上作出点P,使BP+AP的值最小,则BP+AP的值最小,则BP+AP的最小值为______.
的中点,在直径CD上作出点P,使BP+AP的值最小,则BP+AP的值最小,则BP+AP的最小值为______.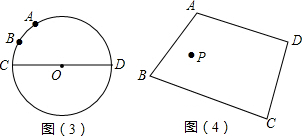
| 3 |
| 3 |
 |
| AC |
 |
| AC |
| 2 |
| 2 |
给出下列四个命题:(1)如果某圆锥的侧面展开图是半圆,则底面半径和母线之比为1:2;(2)若点A在直线y=2x-3上,且点A到两坐标轴的距离相等,则点A在第一或第四象限;
(3)半径为5的圆中,弦AB=8,则圆周上到直线AB的距离为2的点共有四个;(4)若A(a,m)、B(a -1,n)(a 0)在反比例函数
0)在反比例函数 的图象上,则m
的图象上,则m n.其中,正确命题的个数是
n.其中,正确命题的个数是
| A.1个 | B.2个 | C.3个 | D.4个 |
给出下列四个命题:(1)如果某圆锥的侧面展开图是半圆,则底面半径和母线之比为1:2;(2)若点A在直线y=2x-3上,且点A到两坐标轴的距离相等,则点A在第一或第四象限;
(3)半径为5的圆中,弦AB=8,则圆周上到直线AB的距离为2的点共有四个;(4)若A(a,m)、B(a -1,n)(a 0)在反比例函数
0)在反比例函数 的图象上,则m
的图象上,则m n.其中,正确命题的个数是
n.其中,正确命题的个数是
A.1个 B.2个 C.3个 D.4个
 0)在反比例函数
0)在反比例函数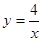 的图象上,则m
的图象上,则m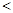 n.其中,正确命题的个数是
n.其中,正确命题的个数是 | A.1个 | B.2个 | C.3个 | D.4个 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com