练习册

  • 练习册
  • 试题
    1． 填空题: (1) 已知圆的直径为13.直线与圆心的距离为.当时.直线与圆 ,当时.直线与圆 . (2) R△ABC中.∠C=90O.AC=3,BC=4.则以C为圆心. 为半径的圆与AB相切,以C为圆心. 为半径的圆与AB相交. (3) 若直线与圆的公共点个数不小于1.则直线与圆的位置关系是 . .A为⊙O的半径OC的延长线上一点,且CA=OC.弦BC=OC.则BC= OA.∠OBA= O .BA与⊙O的位置关系是 . 图(7)图(8) .已知AB是⊙O的直径.延长AB到D.使BD=OB.DC切⊙O于C.则∠D= O.∠C= O.若⊙O的半径为R.则AC= . (6) 两个同心圆的半径分别为1和2.大圆的弦AB与小圆相切.则AB= . (7) 已知I为△ABC的内心.∠B=50O.则∠AIC= . (8) 等边三角形内切圆半径与外切圆半径之比是 . .⊙O内切于R△ABC.∠C=90O.D.E.F为切点.若∠AOC=120O.则∠OAC= O.∠B= O.若AB=2.△ABC的外接圆半径= .内切圆半径=. 【查看更多】

     

    题目列表(包括答案和解析)

    　　作图题：在已知线段AB上求作一点C，使AC∶CB=3∶2(不写作法，保留作图痕迹)．

     

    查看答案和解析>>

    18、补全下列各题解题过程．
    （1）如图1，①∵AD∥BC
    ∴∠FAD=
    ∠ABC
    ．（
    两直线平行，同位角相等
    ）
    ②∵∠1=∠2
    ∴
    AB
    ∥
    CD
    （
    内错角相等，两直线平行
    ）

    （2）如图2，E点为DF上的点，B为AC上的点，
    ∠1=∠2，∠C=∠D，求证DF∥AC．
    证明：∵∠1=∠2（已知）
    ∠2=∠3∠1=∠4 （
    对顶角相等
    ）
    ∴∠3=∠4  （
    等量代换
    ）
    ∴
    DB
    ∥
    CE
     （
    内错角相等，两直线平行
    ）
    ∴∠C=∠ABD  （
    两直线平行，同位角相等
    　）
    ∵∠C=∠D    （
    已知
    　）
    ∴∠D=∠ABD（
    等量代换
    ）
    ∴DF∥AC（
    内错角相等，两直线平行
    ）

    查看答案和解析>>

    某电脑公司现有A,B,C三种型号的甲品牌电脑和D,E两种型号的乙品牌电脑，希望中学要从甲，乙两种品牌电脑中各选购一种型号的电脑。
    【小题1】写出所有的选购方案（利用树状图或列表法表示）；
    【小题2】已知希望中学购买甲，乙两种品牌电脑共36台(价格如图所示)，恰好用去10万元人民币，其中甲品牌电脑为A型电脑，求该学校购买了A型电脑几台？　

    查看答案和解析>>

    如图1，已知∠ABC=90°，△ABE是等边三角形，点P为射线BC上任意一点（点P与点B不重合），连结AP，将线段AP绕点A逆时针旋转60°得到线段AQ，连结QE并延长交射线BC于点F.

    【小题1】如图2，当BP=BA时，∠EBF=　 　°，猜想∠QFC=   °；

    【小题2】如图1，当点P为射线BC上任意一点时，猜想∠QFC的度数，并加以证明
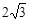    【小题3】已知线段AB=，设BP=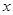，点Q到射线BC的距离为y，求y关于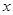的函数关系式．

    查看答案和解析>>

    某公司为了解顾客对自己商品的总体印象，采取随机抽样的方式，对购买了自己商品的年龄在16～65岁之间的400个顾客，进行了抽样调查．并根据每个年龄段抽查人数和该年龄段对商品总体印象感到满意的人数绘制了下面的图(1)和图(2).
    根据上图提供的信息回答下列问题：
    【小题1】被抽查的顾客中，人数最多的年龄段是　　　　　岁；
    【小题2】已知被抽查的400人中有83%的人对商品总体印象感到满意，请你求出31～40岁年龄段的满意人数，并补全图(2)
    【小题3】比较31～40岁和41～50岁这两个年龄段对商品总体印象满意率的高低（四舍五入到1%）．注：某年龄段的满意率＝该年龄段满意人数该年龄段被抽查人数100％．

    查看答案和解析>>


    同步练习册答案