
题目列表(包括答案和解析)
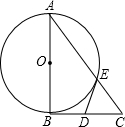 如图所示,△ABC是直角三角形,∠ABC=90°,以AB为直径的⊙O交AC于点E,点D是BC边的中点,连接DE.
如图所示,△ABC是直角三角形,∠ABC=90°,以AB为直径的⊙O交AC于点E,点D是BC边的中点,连接DE.| 3 |
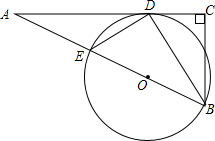 如图所示,在Rt△ABC中,∠C=90°,BC=3,CA=4,∠ABC的角平分线BD交AC于点D,点E是线段AB上的一点,以BE为直径的圆O过点D.
如图所示,在Rt△ABC中,∠C=90°,BC=3,CA=4,∠ABC的角平分线BD交AC于点D,点E是线段AB上的一点,以BE为直径的圆O过点D.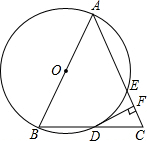 如图所示,已知△ABC中,AB=AC,以AB为直径作⊙O交BC于D,交AC于E,过D作DF⊥AC于F.
如图所示,已知△ABC中,AB=AC,以AB为直径作⊙O交BC于D,交AC于E,过D作DF⊥AC于F. 如图所示,已知△ABC中,AB=AC,以AB为直径作⊙O交BC于D,交AC于E,过D作DF⊥AC于F
如图所示,已知△ABC中,AB=AC,以AB为直径作⊙O交BC于D,交AC于E,过D作DF⊥AC于F 如图所示,以Rt△ABC的直角边AB为直径的⊙O交斜边AC于点E,点D是BC边的中点,连接ED.
如图所示,以Rt△ABC的直角边AB为直径的⊙O交斜边AC于点E,点D是BC边的中点,连接ED.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com