练习册

  • 练习册
  • 试题
    13． 探索.在图12-1至图12-3中.已知△ABC的面积为a ． (1)如图12-1.延长△ABC的边BC到点D.使CD=BC.连结DA．若△ACD的面积为S1.则S1= (用含a的代数式 表示), (2)如图12-2.延长△ABC的边BC到点D.延长边CA到点E.使CD=BC.AE=CA.连结DE．若△DEC的面积为S2.则S2= (用含a的代数式表示), (3)在图12-2的基础上延长AB到点F.使BF=AB.连结FD.FE.得到△DEF．若阴影部分的面积为S3.则S3= (用含a的代数式表示).并运用上述(2)的结论写出理由． 发现 像上面那样.将△ABC各边均顺次延长一倍.连结所得端点.得到△DEF.此时.我们称△ABC向外扩展了一次．可以发现.扩展一次后得到的△DEF的面积是原来△ABC面积的 倍． 应用 要在一块足够大的空地上栽种花卉.工程人员进行了如下的图案设计:首先在△ABC的空地上种红花.然后将△ABC向外扩展三次(图12-4已给出了前两次扩展的图案)．在第一次扩展区域内种黄花.第二次扩展区域内种紫花.第三次扩展区域内种蓝花．如果种红花的区域(即△ABC)的面积是10平方米.请你运用上述结论求出: (1)种紫花的区域的面积, (2)种蓝花的区域的面积． 【查看更多】

     

    题目列表(包括答案和解析)

    如图为羽毛球单打场地按比例缩小的示意图（由图中粗实线表示），它的宽度为5.18米，那么它的长大约在


    1. A.
      12米至13米之间
    2. B.
      13米至14米之间
    3. C.
      14米至15米之间
    4. D.
      15米至16米之间

    查看答案和解析>>

    7、如图，在8×12的网格图中（每个小正方形的边长均为1cm），点A、B在格点上，⊙A、⊙B的半径都为1cm．若⊙A以每秒1cm的速度自左向右运动，与此同时，⊙B的半径在不断增大，它的半径r（cm）与时间t（s）之间的关系式为r=1+t（t≥0），则在网格图范围内，当两圆相切时，t的值为（　　）

    查看答案和解析>>

    （本小题满分10分）
    在图15-1至图15-3中，直线MN与线段AB相交于点O，∠1 = ∠2 = 45°．

    （1）如图15-1，若AO = OB，请写出AO与BD 的数量关系和位置关系；
    （2）将图15-1中的MN绕点O顺时针旋转得到图15-2，其中AO = OB．
    求证：AC = BD，AC ⊥ BD；
    （3）将图15-2中的OB拉长为AO的k倍得到图15-3，求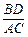的值．

    查看答案和解析>>

    甲、乙两支篮球队在集训期内进行了五场比赛，将比赛成绩进行统计后，绘制成如图12-1、图12-2的统计图．
    （1）在图12-2中画出折线表示乙队在集训期内这五场比赛成绩的变化情况；
    （2）已知甲队五场比赛成绩的平均分=90分，请你计算乙队五场比赛成绩的平均分；
    （3）就这五场比赛，分别计算两队成绩的极差；
    （4）如果从甲、乙两队中选派一支球队参加篮球锦标赛，根据上述统计情况，试从平均分、折线的走势、获胜场数和极差四个方面分别进行简要分析，你认为选派哪支球队参赛更能取得好成绩？

    查看答案和解析>>

    （本小题满分10分）
    在图15-1至图15-3中，直线MN与线段AB相交于点O，∠1 = ∠2 = 45°．

    （1）如图15-1，若AO = OB，请写出AO与BD 的数量关系和位置关系；
    （2）将图15-1中的MN绕点O顺时针旋转得到图15-2，其中AO = OB．
    求证：AC = BD，AC ⊥ BD；
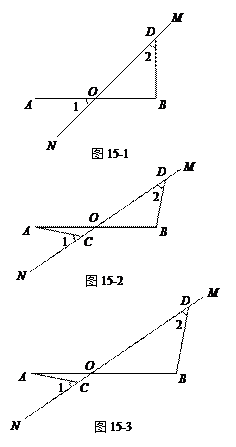
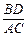    （3）将图15-2中的OB拉长为AO的k倍得到图15-3，求的值．

    查看答案和解析>>


    同步练习册答案