
题目列表(包括答案和解析)
(1)![]() 是关于y的分式方程. ( )
是关于y的分式方程. ( )
(2)分式方程![]() 的解是x=3. ( )
的解是x=3. ( )
(3)只要是分式方程,一定出现增根. ( )
(4)方程![]() 与方程5(x-2)=7x的解相同. ( )
与方程5(x-2)=7x的解相同. ( )
(5)方程![]() 的两边都乘以(x-2),得1=(x-1)-3.( )
的两边都乘以(x-2),得1=(x-1)-3.( )
(6)方程![]() 无解. ( )
无解. ( )
(7)方程![]() 的根为x=0.
( )
的根为x=0.
( )
(8)方程![]() 变形得x=1,而x=1是原方程的增根,故原方程无解.( )
变形得x=1,而x=1是原方程的增根,故原方程无解.( )
先阅读,然后解决问题:
已知:一次函数![]() 和反比例函数
和反比例函数![]() ,求这两个函数图象在同一坐标系内的交点坐标。
,求这两个函数图象在同一坐标系内的交点坐标。
解:解方程-x+2=![]()
去分母,得
-x2+2x=-8
整理得
x2-2x-8=0
解这个方程得:x1=-2 x2=4
经检验,x1=-2 x2=4是原方程的根
当x1=-2,y1=4;x2=4,y2=-2
∴交点坐标为(-2,4)和(4,-2)
问题:
1.在同一直角坐标系内,求反比例函数y= 的图象与一次函数y=x+3的图象的交点坐标;
的图象与一次函数y=x+3的图象的交点坐标;
2.判断一次函数y=2x-3的图象与反比例函数y=-![]() 的图象在同一直角坐标系内有无交点,说明理由.
的图象在同一直角坐标系内有无交点,说明理由.
先阅读,然后解决问题:
已知:一次函数 和反比例函数
和反比例函数 ,求这两个函数图象在同一坐标系内的交点坐标。
,求这两个函数图象在同一坐标系内的交点坐标。
解:解方程-x+2=
去分母,得
-x2+2x=-8
整理得
x2-2x-8=0
解这个方程得:x1=-2 x2=4
经检验,x1=-2 x2=4是原方程的根
当x1=-2,y1=4;x2=4,y2=-2
∴交点坐标为(-2,4)和(4,-2)
问题:
1.在同一直角坐标系内,求反比例函数y= 的图象与一次函数y=x+3的图象的交点坐标;
的图象与一次函数y=x+3的图象的交点坐标;
2.判断一次函数y=2x-3的图象与反比例函数y=- 的图象在同一直角坐标系内有无交点,说明理由.
的图象在同一直角坐标系内有无交点,说明理由.
容积率t是指在房地产开发中建筑面积与用地面积之比,即t=![]() ,为充分利用土地资源,更好地解决人们的住房需求,并适当的控制建筑物的高度,一般地容积率t不小于1且不大于8.一房地产开发商在开发某小区时,结合往年开发经验知,建筑面积M(m2)与容积率t的关系可近似地用如图(1)中的线段l来表示;1 m2建筑面积上的资金投入Q(万元)与容积率t的关系可近似地用如图(2)中的一段抛物线段c来表示.
,为充分利用土地资源,更好地解决人们的住房需求,并适当的控制建筑物的高度,一般地容积率t不小于1且不大于8.一房地产开发商在开发某小区时,结合往年开发经验知,建筑面积M(m2)与容积率t的关系可近似地用如图(1)中的线段l来表示;1 m2建筑面积上的资金投入Q(万元)与容积率t的关系可近似地用如图(2)中的一段抛物线段c来表示.

(1)
试求图(1)中线段l的函数关系式,并求出开发该小区的用地面积;(2)
求出图(2)中抛物线段c的函数关系式.
阅读下列一段话,并解决后面的问题.
观察下面一列数:
1,2,4,8……
我们发现,这一列数从第2项起,每一项与它前一项的比都等于2.
一般地,如果一列数从第2项起,每一项与它前一项的比都等于同一个常数,这一列数就叫做等比数列,这个常数叫做等比数列的公比.
(1)等比数列5,-15,45……的第4项是________;
(2)如果一列数a1,a2,a3,a4,……是等比数列,且公比为q,那么根据上述规定,有
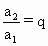 ,
,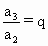 ,
,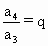 ,……
,……
所以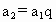 ,
,
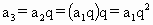 ,
,

……
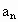 =________.(用a1与q的代数式表示)
=________.(用a1与q的代数式表示)
(3)一个等比数列的第2项是10,第3项是20,求它的第1项与第4项.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com