
题目列表(包括答案和解析)

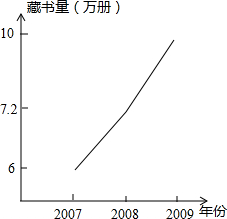 如图是某中学近几年校图书馆藏书量的统计图,从图中看2009年比2008年增加了
如图是某中学近几年校图书馆藏书量的统计图,从图中看2009年比2008年增加了某地为改善生态环境,积极开展植树造林,甲、乙两人从近几年的统计数据中有如下发现:
(1)求y2与x之间的函数关系式?
(2)若上述关系不变,试计算哪一年该地公益林面积可达防护林面积的2倍?这时该地公益林的面积为多少万亩?
某地为改善生态环境,积极开展植树造林,甲、乙两人从近几年的统计数据中有如下发现:

(1)求y2与x之间的函数关系式?
(2)若上述关系不变,试计算哪一年该地公益林面积可达防护林面积的2倍?这时该地公益林的面积为多少万亩?
某地为改善生态环境,积极开展植树造林,甲、乙两人从近几年的统计数据中有如下发现:

(1)求y2与x之间的函数关系式?
(2)若上述关系不变,试计算哪一年该地公益林面积可达防护林面积的2倍?这时该地公益林的面积为多少万亩?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com