2003年我国遭受到非典型肺炎传染疾病的巨大灾难，全国人民万众一心，众志成城，抗击“非典”，如图所示①是根据某市某中学“献爱心，抗非典”自愿捐款活动中学生捐款情况制成的条形图，如图所示②是该中学生人数比例分布图，该学校共有学生1450人．

请回答下列问题：

(1)九年级学生共捐款多少元？

(2)该校学生平均每人捐款多少元？

在2003年，我国内地发生了“非典型性肺炎”疫情，在党和政府的正确领导下，疫情已得到了有效控制．如图所示的是2003年5月11日至5月29日内地新增确诊病例数据走势图(数据来源：卫生部每日疫情通报)，据图回答下列问题：

(1)5月17日新增确诊病例人数为多少？

(2)在5月11日至5月13日三天中，共新增确诊病例的人数为多少？

(3)从图中可以看出，5月下半月新增确诊病例总体是怎样的变化趋势？

解答题．

2003年我国遭受到非典型肺炎传染性疾病的袭击，全国人民万众一心，众志成城，抗击“非典”．图甲是某幢居民楼3个单元捐款情况条形统计图，图乙是3个单元人数比例分布图．该幢居民楼共140人．

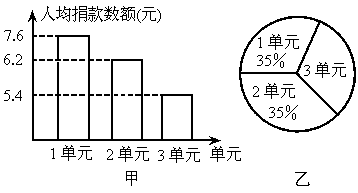
(1)该幢居民楼第3单元共捐款多少元？

(2)该幢居民楼人均捐款多少元？若该小区共有常住居民8 000人，按这个人均捐款额计算，该小区共捐款多少元？

通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的。下面是一个案例，请补充完整。

原题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，试说明理由。

（1）思路梳理

∵AB=CD，

∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合。

∵∠ADC=∠B=90°，

∴∠FDG=180°，点F、D、G共线。

根据　　　　，易证△AFG≌　　　　，得EF=BE+DF。

（2）类比引申

如图2，四边形ABCD中，AB=AD，∠BAD=90°，点E、F分别在边BC、CD上，∠EAF=45°。若∠B、∠D都不是直角，则当∠B与∠D满足等量关系　　　　时，仍有EF=BE+DF。

（3）联想拓展

如图3，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠DAE=45°。猜想BD、DE、EC应满足的等量关系，并写出推理过程。