
题目列表(包括答案和解析)
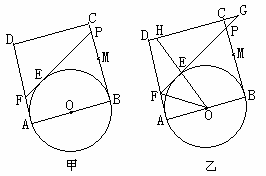
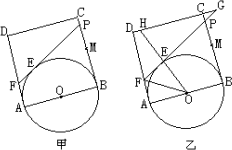
已知,如图(甲),正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点, P不运动到M和C,以AB为直径做⊙O,过点P作⊙O的切线交AD于点F,切点为E.
(1)求四边形CDFP的周长;
(2)试探索P在线段MC上运动时,求AF·BP的值;
(3)延长DC、FP相交于点G,连结OE并延长交直线DC于H(如图乙),是否存在点P,
使△EFO∽△EHG?如果存在,试求此时的BP的长;如果不存在,请说明理由。
已知,如图(甲),正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点,P不运动到M和C,以AB为直径做⊙O,过点P作⊙O的切线交AD于点F,切点为E.
(1)求四边形CDFP的周长;
(2)试探索P在线段MC上运动时,求AF·BP的值;
(3)延长DC、FP相交于点G,连结OE并延长交直线DC于H(如图乙),是否存在点P,使△EFO∽△EHG?如果存在,试求此时的BP的长;如果不存在,请说明理由.
| 5 | 2 |

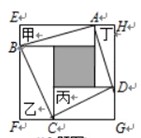
如图,甲,乙,丙,丁四个长方形拼成正方形EFGH,中间阴影为正方形,已知,甲、乙、丙、丁四个长方形面积的和是32cm²,四边形ABCD的面积是20cm²。问甲、乙、丙、丁四个长方形周长的总和是:

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com