
题目列表(包括答案和解析)
将边长OA=8,OC=10的矩形OABC放在平面直角坐标系中,顶点O为原点,顶点C、A分别在 轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠。
轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠。

(1)如图①,当点O落在AB边上的点D处时,点E的坐标为 ;
(2)如图②,当点O落在矩形OABC内部的点D处时,过点E作EG∥ 轴交CD于点H,交BC于点G.求证:EH=CH;
轴交CD于点H,交BC于点G.求证:EH=CH;
(3)在(2)的条件下,设H(m,n),写出m与n之间的关系式 ;
(4)如图③,将矩形OABC变为正方形,OC=10,当点E为AO中点时,点O落在正方形OABC内部的点D处,延长CD交AB于点T,求此时AT的长度。
将边长OA=8,OC=10的矩形OABC放在平面直角坐标系中,顶点O为原点,顶点C、A分别在 轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠。
轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠。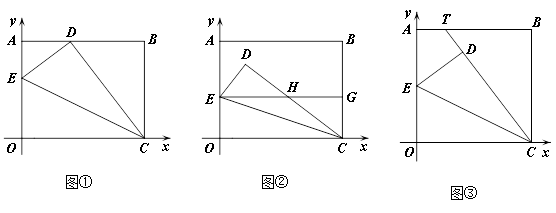
(1)如图①,当点O落在AB边上的点D处时,点E的坐标为 ;
(2)如图②,当点O落在矩形OABC内部的点D处时,过点E作EG∥ 轴交CD于点H,交BC于点G.求证:EH=CH;
轴交CD于点H,交BC于点G.求证:EH=CH;
(3)在(2)的条件下,设H(m,n),写出m与n之间的关系式 ;
(4)如图③,将矩形OABC变为正方形,OC=10,当点E为AO中点时,点O落在正方形OABC内部的点D处,延长CD交AB于点T,求此时AT的长度。
 轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠。
轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠。
 轴交CD于点H,交BC于点G.求证:EH=CH;
轴交CD于点H,交BC于点G.求证:EH=CH;| CE |
| AE |
| 1 |
| 2 |
| CE |
| AE |
| 1 |
| n |
| EF |
| EG |
| 1 |
| n |
| EF |
| EG |
| 1 |
| n |

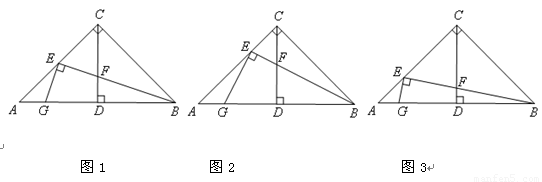
在Rt△ABC中,∠ACB=90 ,AC=BC,CD⊥AB于点D,点E为AC边上一点,联结BE交CD于点F,过点E作EG⊥BE交AB于点G,
,AC=BC,CD⊥AB于点D,点E为AC边上一点,联结BE交CD于点F,过点E作EG⊥BE交AB于点G,
1.如图1,当点E为AC中点时,线段EF与EG的数量关系是 ;
2.如图2,当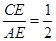 ,探究线段EF与EG的数量关系并且证明;
,探究线段EF与EG的数量关系并且证明;
3.如图3,当 ,线段EF与EG的数量关系是 .
,线段EF与EG的数量关系是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com