练习册

  • 练习册
  • 试题
    如图11-16.矩形ABCD中.对角线AC与BD相交于O点.现将△ABC沿着CD的方向平移.平移距离刚好与CD的长相等.观察平移后的图形.①指出有哪些新的特殊四边形,②并说明这个特殊四边形是什么四边形的理由. C A/ A B C/ 图11-17 A D O B C 图11-16 【查看更多】

     

    题目列表(包括答案和解析)

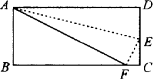
    如图，已知矩形AB－CD沿着AE折叠使D点落在BC边上的F点处，如果∠BAF＝60°，则∠DAE等于

    [　　]

    A．15°

    B．30°

    C．45°

    D．60°

    查看答案和解析>>

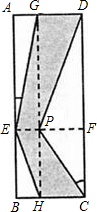    精英家教网如图，从一块矩形薄板ABCD上裁下一个工件GEHCPD（阴影部分）．图中EF∥BC，GH∥AB，∠AEG=11°18′，∠PCF=33°42′，AG=2cm，FC=6cm．求工件GEHCPD的面积．（参考数据：tan11°18'≈
    1
    5
    ，tan33°42′≈
    2
    3
    ）

    查看答案和解析>>

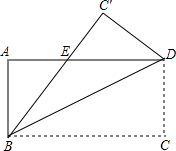    如图，已知矩形ABCD沿着直线BD折叠，使点C落在C′处，BC′交AD于E，AD=16，AB=8，求DE的长．

    查看答案和解析>>

    （2013•嘉定区一模）如图已知△ABC中AB=AC=10，BC=16，矩形DEFG的边EF在△ABC的边BC上，顶点D、G分别在AB、AC上，设DE的长为x，矩形DEFG的面积为y，求y关于x的函数关系式，并写出这个函数的定义域．

    查看答案和解析>>

    （11·佛山）阅读材料

    我们经常通过认识一个事物的局部或其特殊类型，来逐步认识这个事物；

           比如我们通过学习两类特殊的四边形，即平行四边形和梯形（继续学习它们的特殊类型如矩形、等腰梯形等）来逐步认识四边形；

           我们对课本里特殊四边形的学习，一般先学习图形的定义，再探索发现其性质和判定方法，然后通过解决简单的问题巩固所学知识；

    请解决以下问题：

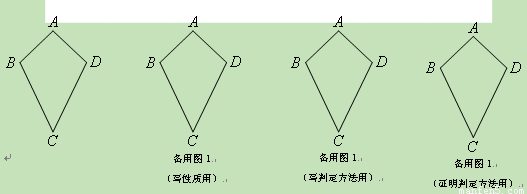
           如图，我们把满足AB＝CD、CB＝CD且AB≠BC的四边形ABCD叫做“筝形”；

    （1）写出筝形的两个性质（定义除外）；

    （2）写出筝形的两个判定方法（定义除外），并选出一个进行证明；

     

    查看答案和解析>>


    同步练习册答案