
题目列表(包括答案和解析)
利用图形来表示数量或数量关系,也可以利用数量或数量关系来描述图形特征或图形之间的关系,这种思想方法称为数形结合.我们刚学过的《从面积到乘法公式》就很好地体现了这一思想方法,你能利用数形结合的思想解决下列问题吗?
如图,一个边长为1的正方形,依次取正方形的 ,根据图示我们可以知道:第一次取走
,根据图示我们可以知道:第一次取走 后还剩
后还剩 ,即
,即 =1﹣
=1﹣ ;前两次取走
;前两次取走 +
+ 后还剩
后还剩 ,即
,即 +
+ =1﹣
=1﹣ ;前三次取走
;前三次取走 +
+ +
+ 后还剩
后还剩 ,即
,即 +
+ +
+ =1﹣
=1﹣ ;…前n次取走后,还剩 _________ ,即 _________ = _________ .
;…前n次取走后,还剩 _________ ,即 _________ = _________ .
利用上述计算:
(1) = _________ .
= _________ .
(2) = _________ .
= _________ .
(3)2﹣22﹣23﹣24﹣25﹣26﹣…﹣22011+22012(本题写出解题过程)
| 分组 | 0﹣19.5 | 19.5﹣39.5 | 39.5﹣59.5 | 59.5﹣79.5 | 79.5﹣100 | 合计 |
| 频数 | 1 | 5 | 6 | 30 | b | 50 |
| 频率 | 0.02 | a | 0.12 | 0.60 | 0.16 | 1 |

利用图形来表示数量或数量关系,也可以利用数量或数量关系来描述图形特征或图形之间的关系,这种思想方法称为数形结合.我们刚学过的《从面积到乘法公式》就很好地体现了这一思想方法,你能利用数形结合的思想解决下列问题吗?
如图,一个边长为1的正方形,依次取正方形的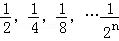 ,根据图示我们可以知道:第一次取走
,根据图示我们可以知道:第一次取走 后还剩
后还剩 ,即
,即 =1﹣
=1﹣ ;前两次取走
;前两次取走 +
+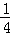 后还剩
后还剩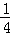 ,即
,即 +
+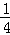 =1﹣
=1﹣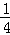 ;前三次取走
;前三次取走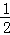 +
+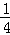 +
+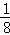 后还剩
后还剩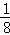 ,即
,即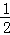 +
+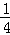 +
+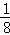 =1﹣
=1﹣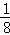 ;…前n次取走后,还剩 _________ ,即 _________ = _________ .
;…前n次取走后,还剩 _________ ,即 _________ = _________ .
利用上述计算:
(1)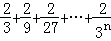 = _________ .
= _________ .
(2)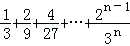 = _________ .
= _________ .
(3)2﹣22﹣23﹣24﹣25﹣26﹣…﹣22011+22012(本题写出解题过程)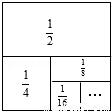
 你根据图表中提供的信息,解答以下问题:
你根据图表中提供的信息,解答以下问题:| 频率分布表 | ||
| 器材种类 | 频数 | 频率 |
| 排 球 | 20 | |
| 乒乓球拍 | 50 | 0.50 |
| 篮 球 | 25 | 0.25 |
| 足 球 | ||
| 合 计 | 1 | |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com