
题目列表(包括答案和解析)
(7分)阅读材料,解答问题:
命题:如图,在锐角△ABC中,BC=a,CA=b,AB=c,ΔABC的外接圆半径为R,
则 2R.
2R. 
证明:连结CO并延长交⊙O于点D,连结DB,则∠D=∠A,因为CD是⊙O的直径,所以∠DBC=900,在Rt△DBC中,sinD= ,所以sinA=
,所以sinA= ,即
,即 ,同理:
,同理: , ∴
, ∴  2R.
2R.
请阅读前面所给的命题和证明后,完成下面(1)(2)两题:
【小题1】(1)前面阅读材料中省略了“ ”的证明过程,请你把“
”的证明过程,请你把“ ”的证明过程补写出来.
”的证明过程补写出来.
【小题2】(2)直接运用阅读材料中命题的结论解题:已知锐角△ABC中, BC= ,CA=
,CA= ,∠A=600,求△ABC的外接圆半径 R及∠C.
,∠A=600,求△ABC的外接圆半径 R及∠C.
(7分)阅读材料,解答问题:
命题:如图,在锐角△ABC中,BC=a,CA=b,AB=c,ΔABC的外接圆半径为R,
则 2R.
2R.

证明:连结CO并延长交⊙O于点D,连结DB,则∠D=∠A,因为CD是⊙O的直径,所以∠DBC=900,在Rt△DBC中,sinD= ,所以sinA=
,所以sinA= ,即
,即 ,同理:
,同理: , ∴
, ∴  2R.
2R.
请阅读前面所给的命题和证明后,完成下面(1)(2)两题:
1.(1)前面阅读材料中省略了“ ”的证明过程,请你把“
”的证明过程,请你把“ ”的证明过程补写出来.
”的证明过程补写出来.
2.(2)直接运用阅读材料中命题的结论解题:已知锐角△ABC中, BC= ,CA=
,CA= ,∠A=600,求△ABC的外接圆半径 R及∠C.
,∠A=600,求△ABC的外接圆半径 R及∠C.
(7分)阅读材料,解答问题:
命题:如图,在锐角△ABC中,BC=a,CA=b,AB=c,ΔABC的外接圆半径为R,
则![]() 2R.
2R.
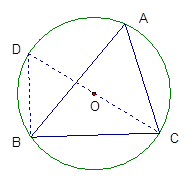
证明:连结CO并延长交⊙O于点D,连结DB,则∠D=∠A,因为CD是⊙O的直径,所以∠DBC=900,在Rt△DBC中,sinD=![]() ,所以sinA=
,所以sinA=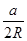 ,即
,即![]() ,同理:
,同理:![]() , ∴
, ∴ ![]() 2R.
2R.
请阅读前面所给的命题和证明后,完成下面(1)(2)两题:
1.(1)前面阅读材料中省略了“![]() ”的证明过程,请你把“
”的证明过程,请你把“![]() ”的证明过程补写出来.
”的证明过程补写出来.
2.(2)直接运用阅读材料中命题的结论解题:已知锐角△ABC中, BC=![]() ,CA=
,CA=![]() ,∠A=600,求△ABC的外接圆半径 R及∠C.
,∠A=600,求△ABC的外接圆半径 R及∠C.
 2R.
2R. 
 ,所以sinA=
,所以sinA= ,即
,即 ,同理:
,同理: , ∴
, ∴  2R.
2R. ”的证明过程,请你把“
”的证明过程,请你把“ ”的证明过程补写出来.
”的证明过程补写出来.  ,CA=
,CA=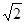 ,∠A=600,求△ABC的外接圆半径 R及∠C.
,∠A=600,求△ABC的外接圆半径 R及∠C.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com