
题目列表(包括答案和解析)
 21、某校数学兴趣小组的同学用学到的解直角三角形知识测量操场上旗杆的高度.如图,在操场上的A处,他们利用测角仪器测得旗杆CD顶端的仰角为23°,再沿AC方向前进20米到达B处,又测得旗杆CD顶端的仰角为36°,已知测角仪器的高度为1.2米,求旗杆CD的高度(精确到0.1米).
21、某校数学兴趣小组的同学用学到的解直角三角形知识测量操场上旗杆的高度.如图,在操场上的A处,他们利用测角仪器测得旗杆CD顶端的仰角为23°,再沿AC方向前进20米到达B处,又测得旗杆CD顶端的仰角为36°,已知测角仪器的高度为1.2米,求旗杆CD的高度(精确到0.1米).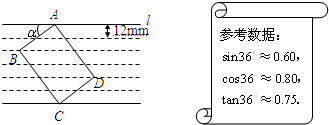
 长为
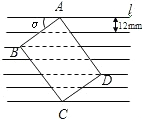
长为(本小题满分8分)小鹏学完解直角三角形知识后,给同桌小艳出了一道题:“如图所示,把一张长方形卡片 放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上,已知
放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上,已知 =36°,求长方形卡片的周长.”请你帮小艳解答这道题.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
=36°,求长方形卡片的周长.”请你帮小艳解答这道题.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
(本题10分)如图,在四边形ABCD中,AB=2,CD=1,∠A=61°,
∠ADC=∠B=90°,利用解直角三角形知识求这个四边形ABCD的面积。
(结果精确到0.1。下列数据供参考:
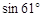 ≈0.87,
≈0.87,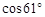 ≈0.48,
≈0.48, ≈1.80;
≈1.80;
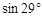 ≈0.48,
≈0.48,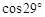 ≈0.87,
≈0.87,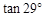 ≈0.55)
≈0.55)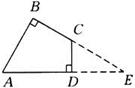
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com