学习了“多边形内角和”这一节后，老师给茗茗留了一道习题，请你帮茗茗完成.

（1）①如图19-1，在△ABC中，∠A=90°，若沿图中虚线剪去∠A，则∠1+∠2的度数为       ；②如图19-2，在△ABC中，∠A=50°，剪去∠A后成四边形，则∠1+∠2的度数为          ；③根据①与②的求解过程，请你猜想∠1+∠2与∠A的关系是                 ；

（2）在（1）中可以知道，一个三角形，通过剪去一个角将它变成四边形时，所得到的新的角和被剪去角之间的关系，如果剪去三角形的两个角，将它变成一个五边形时，剪去的两个角和新的角之间又有怎样的关系？剪去三角形的三个角，将它变成一个六边形时，剪去的三个角和新的角之间又有怎样的关系？

（3）如果将四边形剪去一个角变成五边形，剪去两个角变成六边形，剪去三个角变成七边形，所剪去的角和新角的关系是否与（2）中的相同？如果不同，请说明理由.

 

　　学习了“多边形内角和”这一节后，老师给茗茗留了一道习题，请你帮茗茗完成.

（1）①如图19-1，在△ABC中，∠A=90°，若沿图中虚线剪去∠A，则∠1+∠2的度数为       ；②如图19-2，在△ABC中，∠A=50°，剪去∠A后成四边形，则∠1+∠2的度数为          ；③根据①与②的求解过程，请你猜想∠1+∠2与∠A的关系是                 ；

（2）在（1）中可以知道，一个三角形，通过剪去一个角将它变成四边形时，所得到的新的角和被剪去角之间的关系，如果剪去三角形的两个角，将它变成一个五边形时，剪去的两个角和新的角之间又有怎样的关系？剪去三角形的三个角，将它变成一个六边形时，剪去的三个角和新的角之间又有怎样的关系？

（3）如果将四边形剪去一个角变成五边形，剪去两个角变成六边形，剪去三个角变成七边形，所剪去的角和新角的关系是否与（2）中的相同？如果不同，请说明理由.

 

如图19-3-17，在等腰梯形ABCD中，AB∥CD，AD=BC，∠A=60°，AB=9，CD=5，BC的长是（　　）

图19-3-17

A.3　　　　 B.4　　　　　　 C.5　　　　 D.6

已知任意四边形ABCD，且线段AB、BC、CD、DA、AC、BD的中点分别是E、F、G、H、P、Q.

(1)若四边形ABCD如图19-1-16所示，判断下列结论是否正确.(正确的在括号里填“√”，错误的在括号里填“×”)

甲：顺次连接EF、FG、GH、HE一定会得到平行四边形.(　　)

乙：顺次连接EQ、QG、GP、PE一定会得到平行四边形.(　　)

(2)请选择甲、乙中的一个，证明你对它的判断.

(3)若四边形ABCD如图19-1-17所示，请你判断(1)中的两个结论是否成立?

　　　　　 　　　　

图19-1-16　　　　　　　　　　 图19-1-17

有这样一道习题：已知：如图1，OA和OB是⊙O的半径，并且OA⊥OB，P是OA上任一点(不与O、A重合)，BP的延长线交⊙O于Q，R是OA的延长线上一点，且RP=RQ.说明：RQ为⊙O的切线. （无须证明）

　　请探究下列变化：

　　变化一：交换题设与结论.

如图1，已知OA和OB是⊙O的半径，并且OA⊥OB，P是OA上任一点(不与O、A重合)，BP的延长线交⊙O于Q，过Q点作⊙O的切线交OA的延长线于R.说明：RP=RQ.（要证明）

 

　　　　　

 

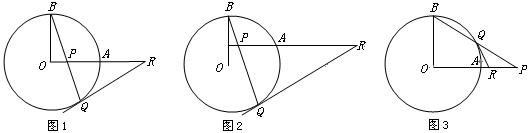
　　变化二：运动探求.

　　(1)如图2，若OA向上平移，变化一中的结论还成立吗？(只需交待判断) 答：_________.

　　(2)如图3，如果P在OA的延长线上时，BP交⊙O于Q，过点Q作⊙O的切线交OA的延长线于R，变化一中的结论还成立吗？为什么？