
题目列表(包括答案和解析)
以下解方程组![]() 的过程是否正确?若不正确应怎样改正?
的过程是否正确?若不正确应怎样改正?
解:由原方程可得:
![]() 或
或![]()
解得![]() 或
或
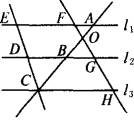
A.由AB=BC可得FG=GH
B.由AB=BC可得OB=OG
C.由CE=2CD可得CA=2BC
D.由GH=FH可得CD=DE
如图,直线AB与CD相交于点O,OE⊥AB,
 OF⊥CD,OP是∠BOC的平分线。
OF⊥CD,OP是∠BOC的平分线。
(1)如果∠AOD=40°,
①那么根据 ,可得∠BOC= °.
②因为OP是∠BOC的平分线,所以∠BOP= °.
③求得∠BOF= °.
(2)∠AOD的余角是 ;∠AOD的补角是 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com