
题目列表(包括答案和解析)
解:这只船的顺水速是( )千米/时,逆水速是( )千米/时,若设水流速为x千米/时,列方程为( ),解x=( ).船在静水中的速度为( )千米/时.
解:18分钟=__________
设经过x小时追上小丁
小明18分钟的路程为______.
小明以10千米/时的速度走完这段路程回到家所用的时间为______小时.
小丁从出发到被小明追上一共用了__________小时.
小丁在这段时间内所走的路程为______千米.
这是小明要追路程
因此列方程为__________
解方程__________
∴小明需用__________小时追上小丁.
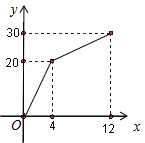 ,在随后的8分钟内既进水又出水,得到x(分)与水量y(升)之间的关系如图:
,在随后的8分钟内既进水又出水,得到x(分)与水量y(升)之间的关系如图: 万吨•千米)尽可能小.
万吨•千米)尽可能小.| 地区 水库 |
甲 | 乙 | 总计 |
| A | x | 14-x 14-x |
14 |
| B | 15-x 15-x |
x-1 x-1 |
14 |
| 总计 | 15 | 13 | 28 |
|
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com