
题目列表(包括答案和解析)
已知a是方程x2+x-![]() =0的根,求
=0的根,求![]() 的值.
的值.
解:由题意,构造关于a的一元二次方程得a2+a-![]() =0.
=0.
即a2=![]() -a,a2+a=
-a,a2+a=![]() .
.
于是![]() =
=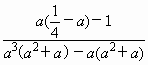
=
=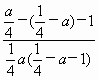
=![]()
=20.
请你构造一个一元二次方程解下列题目:
已知x=-![]() ,求
,求![]() 的值.
的值.
| 2 |
| 2 |
| 2 |
| 2 |
| 5 |
| 5 |
阅读下列材料,按要求解答问题:
如图2-1,在ΔABC中,∠A=2∠B,且∠A=60°.小明通过以下计算:由题意,∠B=30°,∠C=90°,c=2b,a=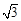 b,得a2-b2=(
b,得a2-b2=(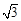 b)2-b2=2b2=b·c.即a2-b2= bc.
b)2-b2=2b2=b·c.即a2-b2= bc.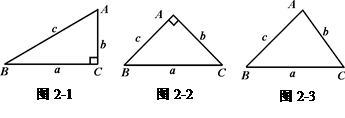
于是,小明猜测:对于任意的ΔABC,当∠A=2∠B时,关系式a2-b2=bc都成立.
(1)如图2-2,请你用以上小明的方法,对等腰直角三角形进行验证,判断小明的猜测是否正确,并写出验证过程;
(2)如图2-3,你认为小明的猜想是否正确,若认为正确,请你证明;否则,请说明理由;
(3)若一个三角形的三边长恰为三个连续偶数,且∠A=2∠B,请直接写出这个三角形三边的长,不必说明理由.
 b,得a2-b2=(
b,得a2-b2=( b)2-b2=2b2=b·c.即a2-b2= bc.
b)2-b2=2b2=b·c.即a2-b2= bc.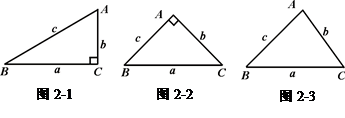
阅读下列材料,按要求解答问题:
如图2-1,在ΔABC中,∠A=2∠B,且∠A=60°.小明通过以下计算:由题意,∠B=30°,∠C=90°,c=2b,a=![]() b,得a2-b2=(
b,得a2-b2=(![]() b)2-b2=2b2=b·c.即a2-b2= bc.
b)2-b2=2b2=b·c.即a2-b2= bc.

于是,小明猜测:对于任意的ΔABC,当∠A=2∠B时,关系式a2-b2=bc都成立.
(1)如图2-2,请你用以上小明的方法,对等腰直角三角形进行验证,判断小明的猜测是否正确,并写出验证过程;
(2)如图2-3,你认为小明的猜想是否正确,若认为正确,请你证明;否则,请说明理由;
(3)若一个三角形的三边长恰为三个连续偶数,且∠A=2∠B,请直接写出这个三角形三边的长,不必说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com