
题目列表(包括答案和解析)

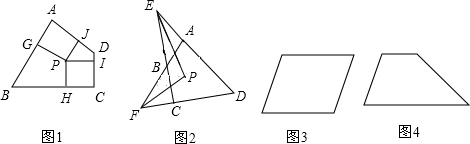
定义:到凸四边形一组对边距离相等,到另一组对边距离也相等的点叫凸四边形的准内点.如图1,![]() ,
,![]() ,则点
,则点![]() 就是四边形
就是四边形![]() 的准内点.
的准内点.
 | |||
 | |||
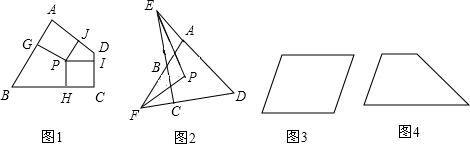
(1)如图2, ![]() 与
与![]() 的角平分线
的角平分线![]() 相交于点
相交于点![]() .
.
求证:点![]() 是四边形
是四边形![]() 的准内点.
的准内点.
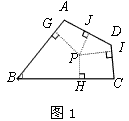
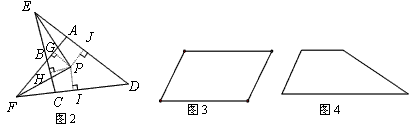
(2)分别画出图3平行四边形和图4梯形的准内点.
(作图工具不限,不写作法,但要有必要的说明)
(3)判断下列命题的真假,在括号内填“真”或“假”.
①任意凸四边形一定存在准内点.( )
②任意凸四边形一定只有一个准内点.( )
③若![]() 是任意凸四边形
是任意凸四边形![]() 的准内点,则
的准内点,则![]()
或![]() .( )
.( )
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com