
题目列表(包括答案和解析)
等腰梯形的有关性质:等腰梯形是一个________对称图形;等腰梯形同一底边上的两个内角________;等腰梯形的两条对角线________.
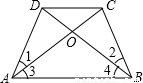
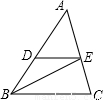
①从角看:在同一底上的两个角________________________________________________;
②从边看:两腰_____________________________________________________________;
③从对角线看:两条对角线___________________________________________________;
④从图形的对称性看:是________对称图形.
 AC•BD.
AC•BD.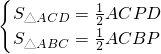
 AC•PD+
AC•PD+ AC•BP
AC•BP AC(PD+PB)=
AC(PD+PB)= AC•B D
AC•B D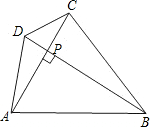
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com