在数学文化节第一轮活动中，我们以探讨一个趣题的方式纪念了数学大师欧拉诞辰300周年．著名数学家拉普拉斯说过：“读读欧拉，他是我们所有人的导师．”是啊！欧拉在数学上的贡献实在太多了，即使在初等数学中也到处可见他的身影．我们再来看看欧拉研究过的“36军官问题”：
从6支部队中各选出6名不同军衔的军官，将这36名军官排成一个6行6列的方阵，要求每行每列的6个军官分别来自不同的部队，并具有不同的军衔．用大写字母A，B，C，D，E，F分别表示6支不同的部队，用小写字母a，b，c，d，e，f分别表示6种不同的军衔，于是问题转化为：在6×6的方格阵中，每个方格分别填入一个大写字母和一个小写字母，使每行和每列中的大小写字母只能各出现一次（通常称这种方阵为欧拉方阵或正交拉丁方）．欧拉搅尽脑汁，也没能排出符合要求的6×6方阵，他猜想并不存在这样的6×6方阵．100多年以后，才有人证明了欧拉的这个猜想是正确的．
于是欧拉继而探究了其他情形，例如，他分别作出了3×3，4×4，5×5正交拉丁方，并证明了当n除以4的余数不等于2时，n×n正交拉丁方是存在的．
正交拉丁方在药品配方试验设计等方面有着广泛应用．现在流行的“数独”游戏和比赛，就是发源于拉丁方问题呢！
如图是一个5×5正交拉丁方，请将剩余的字母填上
．
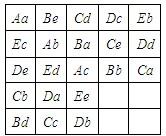
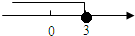14、某不等式的解集如图，则这个解集用不等式表示为
