解:方案(1) 画法1: 画法2: 画法3: 过F作FH∥AB交 (1)在——青夏教育精英家教网—

解:方案(1) 画法1: 画法2: 画法3: 过F作FH∥AB交 (1)在AD上取一点 AD于点H AD于点H H.使DH=CF (2)在DC上任取一点G 在CD上任取连接EF.FG.GH. DC于点G 一点G HE.则四边形EFGH 连接EF.FG.GH. 连接EF.FG.GH. 就是所要画的四边形, HE.则四边形EFGH HE.则四边形EFGH 就是所要画的四边形就是所要画的四边形 (画图正确得4分.简要说明画法得1分) 方案过M点作MP∥AB交AD于点P. (2)在AB上取一点Q.连接PQ. (3)过M作MN∥PQ交DC于点N. 连接QM.PN.MN 则四边形QMNP就是所要画的四边形 (画图正确的2分.简要说明画法得1分) 【查看更多】

已知：图（1）、图（2）分别是6×6正方形网格上两个轴对称图形（阴影部分），其面积分别为S_A、SB（网格中最小的正方形面积为一个平方单位），请观察图形并解答下列问题.

(1）填空：SA∶SB的值是__________；

(2）请你在图（3）的网格上画出一个面积为8个平方单位的中心对称图形.

提示：如果没有规律性认识，要找出具有撁栏袛的图案是比较困难的，适当的方法是：选择一些图形作为基本图形，通过基本图形的组合，找出解答，所列的7个图形可认为是基本图形.

请你再作出3个符合要求的图形.

查看答案和解析>>

直角三角形通过剪切可以拼成一个与该直角三角形面积相等的矩形．方法如下：

请你用上面图示的方法，解答下列问题：(在原图上画出，并仿照例题作必要的标注)

(1)对任意三角形，设计一种方案，将它分成若干块，再拼成一个与原三角形面积相等的矩形．

(2)对任意四边形，设计一种方案，将它分成若干块，再拼成一个与原四边形面积相等的矩形．

查看答案和解析>>

本题有2个小题，请你从中任选一题作答，如果两题都作答，你会浪费一部分时间！我们将按解答完整的题给分．
测量路灯的高度或河的宽度．说明：
①测量可以在有阳光的晴日里进行．
②测量者只备有若干根标竿及测量长度用的皮卷尺．
③画出相关图形，用a、b、c …等表示测量所得的数据．
题（1）小明和爸爸一起散步，发现小区新安装了漂亮的路灯．决定测量一下路灯的高度．请你帮助小明设计一个测量方案，并说明理由．
题（2）灵山乐园中的人工河欲建一座观赏桥，由于受条件限制，无法直接度量A、B间的距离（AB垂直河岸，河岸大致平行，B处这边是宽阔的平地），请你用学过的知识，设计一个测量方案，并说明理由．

查看答案和解析>>

本题有2个小题，请你从中任选一题作答，如果两题都作答，你会浪费一部分时间！我们将按解答完整的题给分．
测量路灯的高度或河的宽度．说明：
①测量可以在有阳光的晴日里进行．
②测量者只备有若干根标竿及测量长度用的皮卷尺．
③画出相关图形，用a、b、c …等表示测量所得的数据．
题（1）小明和爸爸一起散步，发现小区新安装了漂亮的路灯．决定测量一下路灯的高度．请你帮助小明设计一个测量方案，并说明理由．
题（2）灵山乐园中的人工河欲建一座观赏桥，由于受条件限制，无法直接度量A、B间的距离（AB垂直河岸，河岸大致平行，B处这边是宽阔的平地），请你用学过的知识，设计一个测量方案，并说明理由．

查看答案和解析>>

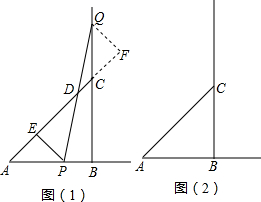（1）等腰△ABC的直角边AB=BC=10cm，点P、Q分别从A、C两点同时出发，均以1cm/秒的相同速度作直线运动，已知P沿射线AB运动，Q沿边BC的延长线运动，PQ与直线AC相交于点D，过P作PE⊥AC于点E．设P点运动时间为t．
①当点P在线段AB上运动时，线段DE的长度是否改变？若不改变，求出DE的值；若改变，请说明理由．
下面给出一种解题的思路，你可以按这一思路解题，也可以选择另外的方法解题．
解：过Q作QF⊥直线AC于点M
∵PE⊥AC于点E，QF⊥直线AC于点M
∴∠AEP=∠F=90°
（下面请你完成余下的解题过程）
②当点P在线段AB的延长线上运动时，（1）中的结论是否还成立？请在图2画出图形并说明理由．
（2）若将（1）中的“腰长为10cm的等腰直角△ABC”改为“边长为a的等边△ABC”时（其余条件不变），则线段DE的长度又如何？（直接写出答案，不需要解题过程）
（3）若将（2）中的“等边△ABC”改为“△ABC”（其余条件不变），请你做出猜想：当△ABC满足

∠A=∠ACB

条件时，（2）中的结论仍然成立．（直接写出答案，不需要解题过程）

查看答案和解析>>

练习册

高中

初中

小学