
题目列表(包括答案和解析)
下面是小明对多项式 进行因式分解的过程.
进行因式分解的过程.
解:设 .
.
原式= (第一步)
(第一步)
= (第二步)
(第二步)
= (第三步)
(第三步)
= (第四步)
(第四步)
回答下列问题:
(1)小明从第二步到第三步运用了因式分解的 .
| A.提取公因式 | B.平方差公式 |
| C.两数和的完全平方公式 | D.两数差的完全平方公式 |
 进行因式分解.
进行因式分解.下面是小明对多项式 进行因式分解的过程.
进行因式分解的过程.
解:设 .
.
原式= (第一步)
(第一步)
= (第二步)
(第二步)
= (第三步)
(第三步)
= (第四步)
(第四步)
回答下列问题:
(1)小明从第二步到第三步运用了因式分解的 .
A.提取公因式 B.平方差公式
C.两数和的完全平方公式 D.两数差的完全平方公式
(2)小明因式分解的结果是否彻底?答: (填“彻底”或“不彻底”);若不彻底,请直接写出因式分解的最后结果 .
(3)请你模仿以上方法尝试对多项式 进行因式分解.
进行因式分解.
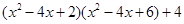 进行因式分解的过程.
进行因式分解的过程.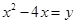 .
.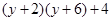 (第一步)
(第一步) 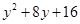 (第二步)
(第二步)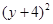 (第三步)
(第三步)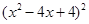 (第四步)
(第四步)| A.提取公因式 | B.平方差公式 |
| C.两数和的完全平方公式 | D.两数差的完全平方公式 |
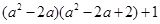 进行因式分解.
进行因式分解.下面是小明对多项式![]() 进行因式分解的过程.
进行因式分解的过程.
解:设![]() .
.
原式=![]() (第一步)
(第一步)
=![]() (第二步)
(第二步)
=![]() (第三步)
(第三步)
=![]() (第四步)
(第四步)
回答下列问题:
(1)小明从第二步到第三步运用了因式分解的 ▲ .
A.提取公因式 B.平方差公式
C.两数和的完全平方公式 D. 两数差的完全平方公式
(2)小明因式分解的结果是否彻底?答: ▲ (填“彻底”或“不彻底”);若不彻底![]() ,请直接写出因式分解的最后结果 ▲ .
,请直接写出因式分解的最后结果 ▲ .
(3)请你模仿以上方法尝试对多项式![]() 进行因式分解.
进行因式分解.
| 1 |
| 3 |
| 46 |
| 3 |
| 1 |
| 8 |
| 46 |
| 24 |
| 23 |
| 12 |
| 11 |
| 12 |
| 1 |
| 3 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 3 |
| 1 |
| 8 |
| 15×3+1 |
| 24 |
| 11 |
| 12 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 12 |
| 11 |
| 12 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com