练习册

  • 练习册
  • 试题
    25．解:(1)①如图11.作AE⊥PB于点E． - - - - - - - - - - - - -1分 ∵ △APE中.∠APE=45°.. ∴ . ． ∵ . ∴ ．- - - - - - - - - - - - - - - - - - 2分 在Rt△ABE中.∠AEB=90°. ∴ ．- - - - - - - - - - - - -3分 ②解法一:如图12.因为四边形ABCD为正方形.可将 △PAD绕点A顺时针旋转90°得到△. 可得△≌△.,． ∴ =90°.=45°.=90°． ∴ ．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 4分 ∴ ．- - - - - - - - - - - - - -5分 解法二:如图13.过点P作AB的平行线.与DA的延长线交于F.设DA的 延长线交PB于G． 在Rt△AEG中.可得 . .． 在Rt△PFG中.可得.． - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 4分 在Rt△PDF中.可得 ． - - - - - - - - - - - - - - - - -5分 (2)如图14所示.将△PAD绕点A顺时针旋转90°得到△. PD 的最大值即为的最大值. ∵ △中.... 且P.D两点落在直线AB的两侧. ∴ 当三点共线时.取得最大值. 此时.即的最大值为6.- - - - - - - - - - - - - - - - - - - - - - - 6分 此时∠APB=180°-=135°.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 7分 【查看更多】

     

    题目列表(包括答案和解析)

    解：如图所示，过点A、D分别作BC的垂线AE、DF分别交BC于点E、F，------1分

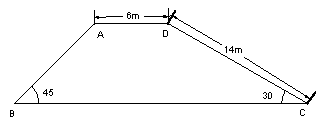    所以△ABE、△CDF均为Rt△，

    又因为CD＝14，∠DCF＝30°，

    所以DF＝7＝AE，-----------------------4分

    所以FC＝7≈12.1 ------------------6分

    所以BC＝7＋6＋12.1＝25.1m．------8分

    查看答案和解析>>

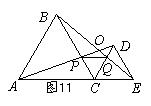
    如图11，C为线段AE上一动点（不与点A、E重合），在AE同侧分别作正三角形ABC和正三角形CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连结PQ，以下五个结论：

    ①AD=BE  ②PQ∥AE  ③AP=BQ  ④DE=DP  ⑤∠AOB=60°

    恒成立的结论有          （填序号）.

    查看答案和解析>>

    数学课上，张老师出示了如下框中的题目．

    小聪与同桌小明讨论后，进行了如下解答：

    (1)特殊情况，探索结论

    当点E为AB的中点时，如图，确定线段AE与DB的大小关系，请你直接写出结论：

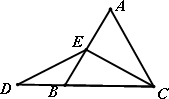
    AE________DB(填“＞”，“＜”或“＝”)．

    (2)特例启发，解答题目

    解：题目中，AE与DB的大小关系是：AE________DB(填“＞”，“＜”或“＝”)．理由如下：如图，过点E作EF∥BC，交AC于点F．

    (请你完成以下解答过程)

    (3)拓展结论，设计新题

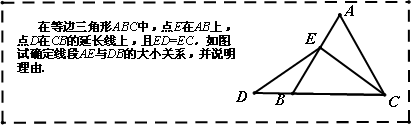
    在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED＝EC．

    若△ABC的边长为1，AE＝2，求CD的长(请你直接写出结果)．

    查看答案和解析>>

    数学课上，陈老师出示了如下框中的题目．

    小敏与同桌小聪讨论后，进行了如下解答：

    (1)特殊情况，探索结论

    当点E为AB的中点时，如图，确定线段AE与DB的大小关系，请你直接写出结论：AE________DB(填“＞”，“＜”或“＝”)．

    (2)一般情况，启发解答

    解：题目中，AE与DB的大小关系是：AE________CB(填“＞”，“＜”或“＝”)．理由如下：如图，过点E作EF∥BC，交AC于点F．

    (请你完成以下解答过程)

    查看答案和解析>>

    已知直线AB∥CD，直线EF与AB、CD分别相交于点E、F．
    （1）如图1，若∠1=60°，求∠2、∠3的度数；
    （2）若点P是平面内的一个动点，连结PE、PF，探索∠EPF、∠PEB、∠PFD三个角之间的关系：
    ①当点P在图2的位置时，可得∠EPF=∠PEB+∠PFD；
    请阅读下面的解答过程，并填空（理由或数学式）．
    解：如图2，过点P作MN∥AB，
    则∠EPM=∠PEB
    （两直线平行，内错角相等）
    （两直线平行，内错角相等）

    ∵AB∥CD（已知），MN∥AB（作图），
    ∴MN∥CD
    （如果两条直线都和第三条直线平行，那么这两条直线也互相平行）
    （如果两条直线都和第三条直线平行，那么这两条直线也互相平行）

    ∴∠MPF=∠PFD
    （两直线平行，内错角相等）
    （两直线平行，内错角相等）

    ∴
    ∠EPM+∠FPM
    ∠EPM+∠FPM
    =∠PEB+∠PFD（等式的性质）
    即∠EPF=∠PEB+∠PFD．
    ②当点P在图3的位置时，请直接写出∠EPF、∠PEB、∠PFD三个角之间的关系：
    ∠EPF+∠PEB+∠PFD=360°
    ∠EPF+∠PEB+∠PFD=360°
    ；
    ③当点P在图4的位置时，请直接写出∠EPF、∠PEB、∠PFD三个角之间的关系：
    ∠EPF+∠PFD=∠PEB
    ∠EPF+∠PFD=∠PEB
    ．

    查看答案和解析>>


    同步练习册答案