
题目列表(包括答案和解析)
| M(l) |
| M(l) |
| M(m) |
| M(m) |

| M(l) |
| M(l) |
| M(m) |
| M(m) |
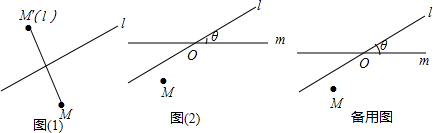
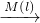 M′(l),点M的轴对称点就记为M′(l),如图(1)所示.如果先作平面上的点M关于直线l的轴对称变换,M
M′(l),点M的轴对称点就记为M′(l),如图(1)所示.如果先作平面上的点M关于直线l的轴对称变换,M M′(l),M得到对应点M′(l),然后,再作M′(l)关于另外一条直线m的轴对称变换,M′(l)
M′(l),M得到对应点M′(l),然后,再作M′(l)关于另外一条直线m的轴对称变换,M′(l) M″(l,m),这样点M就与该点关于直线l和m的轴对称点M″(l,m)之 间建立了一种对应关系,我们把这种对应关系就叫做点M关于直线l和m的轴对称变换,M′(l)
M″(l,m),这样点M就与该点关于直线l和m的轴对称点M″(l,m)之 间建立了一种对应关系,我们把这种对应关系就叫做点M关于直线l和m的轴对称变换,M′(l)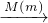 M″(l,m),记为,M的对应点就记为M″(l,m).如图(2),M是平面上的一点,直线l、m相交所成的角为θ(0°<θ≤90°),且交点为O,请回答如下问题:
M″(l,m),记为,M的对应点就记为M″(l,m).如图(2),M是平面上的一点,直线l、m相交所成的角为θ(0°<θ≤90°),且交点为O,请回答如下问题:
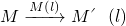 ,点M的轴对称点就记为M′(l),如图(1)所示.如果先作平面上的点M关于直线l的轴对称变换
,点M的轴对称点就记为M′(l),如图(1)所示.如果先作平面上的点M关于直线l的轴对称变换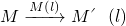 ,得到对应点M′(l),然后,再作M′(l)关于另外一条直线m的轴对称变换
,得到对应点M′(l),然后,再作M′(l)关于另外一条直线m的轴对称变换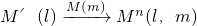 ,这样点M就与该点关于直线l和m的轴对称点M′′(l,m)之间建立了一种对应关系,我们把这种对应关系就叫做点M关于直线l和m的轴对称变换,记为
,这样点M就与该点关于直线l和m的轴对称点M′′(l,m)之间建立了一种对应关系,我们把这种对应关系就叫做点M关于直线l和m的轴对称变换,记为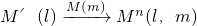 ,M的对应点就记为M′′(l,m).如图(2),M是平面上的一点,直线l、m相交所成的角为θ(0°<θ≤90°),且交点为O,请回答如下问题:
,M的对应点就记为M′′(l,m).如图(2),M是平面上的一点,直线l、m相交所成的角为θ(0°<θ≤90°),且交点为O,请回答如下问题:
 M′(l),点M的轴对称点就记为M′(l),如图(1)所示.如果先作平面上的点M关于直线l的轴对称变换,M
M′(l),点M的轴对称点就记为M′(l),如图(1)所示.如果先作平面上的点M关于直线l的轴对称变换,M M′(l),M得到对应点M′(l),然后,再作M′(l)关于另外一条直线m的轴对称变换,M′(l)
M′(l),M得到对应点M′(l),然后,再作M′(l)关于另外一条直线m的轴对称变换,M′(l) M″(l,m),这样点M就与该点关于直线l和m的轴对称点M″(l,m)之 间建立了一种对应关系,我们把这种对应关系就叫做点M关于直线l和m的轴对称变换,M′(l)
M″(l,m),这样点M就与该点关于直线l和m的轴对称点M″(l,m)之 间建立了一种对应关系,我们把这种对应关系就叫做点M关于直线l和m的轴对称变换,M′(l) M″(l,m),记为,M的对应点就记为M″(l,m).如图(2),M是平面上的一点,直线l、m相交所成的角为θ(0°<θ≤90°),且交点为O,请回答如下问题:
M″(l,m),记为,M的对应点就记为M″(l,m).如图(2),M是平面上的一点,直线l、m相交所成的角为θ(0°<θ≤90°),且交点为O,请回答如下问题:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com