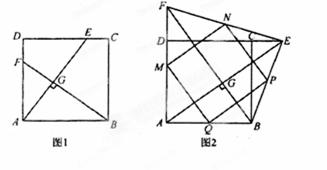
如图1，正方形ABCD中，点E、F分别在边DC、AD上，且AE⊥BF于G.

（1）求证：BF＝AE

（2）如图2，当点E在DC延长线上，点F在AD延长线上时，（1）中结论是否成立（直接写结论）

（3）在图2中，若点M、N、P、Q分别为四边形AFEB四条边AF、EF、EB、AB的中点，且AF:AD＝4:3，求S_{四边形MNPQ}: S_{正方形ABCD}（本小题10分）

(本题满分11分)
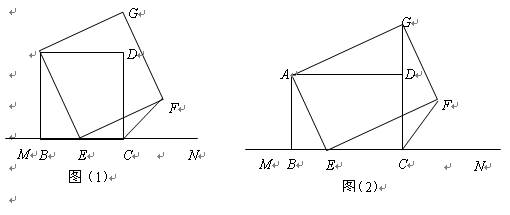
如图（1），已知正方形ABCD在直线MN的上方，BC在直线MN上，E是BC上一点，以AE为边在直线MN的上方作正方形AEFG．
【小题1】（1）连接GD，求证：△ADG≌△ABE；(2分)
【小题2】（2）连接FC，观察并猜测∠FCN的度数，并说明理由；(3分)
【小题3】（3）如图（2），将图（1）中正方形ABCD改为矩形ABCD，AB=a，BC=b（a、b为常数），E是线段BC上一动点（不含端点B、C），以AE为边在直线MN的上方作矩形AEFG，使顶点G恰好落在射线CD上．判断当点E由B向C运动时，∠FCN的大小是否总保持不变，若∠FCN的大小不变，请用含a、b的代数式表示tan∠FCN的值；若∠FCN的大小发生改变，请举例说明．(4分)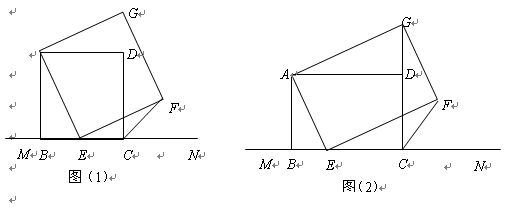

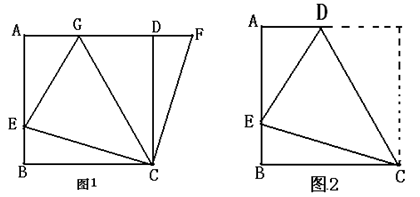
（本题满分8分）如图，在正方形ABCD中，E是AB边上任意一点，BG⊥CE，垂足为点O,交AC于点F，交AD于点G。

（1）证明：BE=AG ；

（2）点E位于什么位置时，∠AEF=∠CEB，说明理由。