
题目列表(包括答案和解析)
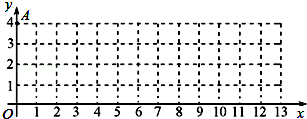
如图,在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫做整点.已知点A(0,4),点B(4n,0)(n为正整数),记△AOB内部(不包括边界)的整点个数为m.则m等于( )

A.3n????????????? B.3n-2???????? C.6n+2?????????? D.6n-3
| A.3n | B.3n-2 | C.6n+2 | D.6n-3 |
 .
.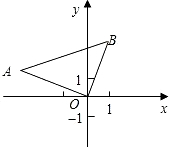 .
.在平面直角坐标系中,△AOB的位置如图所示,已知∠AOB=90º,AO=BO,点A的坐标为(-3,1).

(1)求点B的坐标;
(2)求过A,O,B三点的抛物线的解析式;
(3)设抛物线的对称轴为直线![]() ,P是直线
,P是直线![]() 上的一点,且△PAB的面积等于△AOB.求点P的坐标。
上的一点,且△PAB的面积等于△AOB.求点P的坐标。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com