
题目列表(包括答案和解析)
如图,函数y1=x+1的图象与反比例函数y2=![]() (k为常数,且k≠0)的图象都经过点A(m,2).
(k为常数,且k≠0)的图象都经过点A(m,2).
(1)求点A的坐标及反比例函数的表达式;
(2)结合图象直接比较:当x>0时,y1与y2的大小.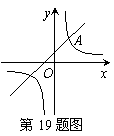
如图,函数y=![]() (x>0,k为常数)的图象经过A(1,4),B(m,n),其中m>1,过点B作y轴的垂线,垂足为D,连结AD.
(x>0,k为常数)的图象经过A(1,4),B(m,n),其中m>1,过点B作y轴的垂线,垂足为D,连结AD.
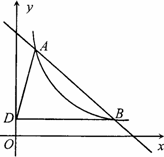
(1)求k的值;
(2)若△ABD的面积为4,求点B的坐标;并回答当x取何值时,直线AB的图象在反比例函数y=![]() 图象的上方.
图象的上方.
反比例函数y1=![]() 图象上的一些点的坐标如下表所示:
图象上的一些点的坐标如下表所示:
| x | … | -3 | -2 | -1 | … | 1 | 2 | 3 | … |
| y | … | 2 | 3 | 6 | … | -6 | -3 | -2 | … |
(1)这个反比例函数的表达式是 ;
(2)一次函数的表达式是y2=mx-1(其中,m是常数,且m≠0).
①求证:不论m为何值,该一次函数的图象都经过一个定点;
②已知一次函数的图象与反比例函数图象交于点(-6,1)和点(3,-2),请你直接写出使式子
![]() >mx-1成立的x的取值范围.
>mx-1成立的x的取值范围.
如图,在直角坐标平面内,函数![]() (x>0,m是常数)的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连结AD,DC,CB.
(x>0,m是常数)的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连结AD,DC,CB.
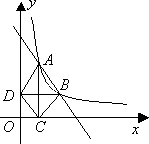
(1)若△ABD的面积为4,求点B的坐标;
(2)求证:DC∥AB;
(3)当AD=BC时,求直线AB的函数解析式.
如图1,平面之间坐标系中,等腰直角三角形的直角边BC在x轴正半轴上滑动,点C的坐标为(t,0),直角边AC=4,经过O,C两点做抛物线y1=ax(x-t)(a为常数,a>0),该抛物线与斜边AB交于点E,直线OA:y2=kx(k为常数,k>0)

(1)填空:用含t的代数式表示点A的坐标及k的值:A________,k=________;
(2)随着三角板的滑动,当a=![]() 时:
时:
①请你验证:抛物线y1=ax(x-t)的顶点在函数y=-![]() x2的图象上;
x2的图象上;
②当三角板滑至点E为AB的中点时,求t的值;
(3)直线OA与抛物线的另一个交点为点D,当t≤x≤t+4,|y2-y1|的值随x的增大而减小,当x≥t+4时,|y2-y1|的值随x的增大而增大,求a与t的关系式及t的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com