
题目列表(包括答案和解析)
(1)解:在△AOC中,AC=4,
∵ AO=OC=4,
∴ △AOC是等边三角形.………1分
∴ ∠AOC=60°,
∴∠AEC=30°.…………………3分
(2)证明:∵OC⊥l,BD⊥l.
∴ OC∥BD. ……………………4分
∴ ∠ABD=∠AOC=60°.
∵ AB为⊙O的直径,
∴ △AEB为直角三角形,∠EAB=30°. …………………………7分
∴∠EAB=∠AEC.
∴ 四边形OBEC 为平行四边形. …………………………………6分
又∵ OB=OC=4.
∴ 四边形OBEC是菱形. …………………………………………7 分
 (2013•浙江一模)如图,在△AOC中,AC=OC,O是坐标原点,点C在x轴上,点A坐标是(1,3),则点C的坐标是
(2013•浙江一模)如图,在△AOC中,AC=OC,O是坐标原点,点C在x轴上,点A坐标是(1,3),则点C的坐标是| k |
| x |
| 2 |
| 3 |
| 2 |
| 3 |
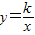 (x>0)上,AC与双曲线交于点B,点E是线段OA上一点(不与O,A重合),设点D(m,0)是x轴正半轴上的一个动点,且满足∠BED=∠AOC,当线段OA上符合条件的点E有且仅有2个时,m的取值范围是 .
(x>0)上,AC与双曲线交于点B,点E是线段OA上一点(不与O,A重合),设点D(m,0)是x轴正半轴上的一个动点,且满足∠BED=∠AOC,当线段OA上符合条件的点E有且仅有2个时,m的取值范围是 .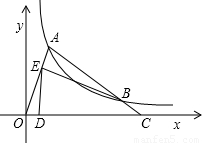
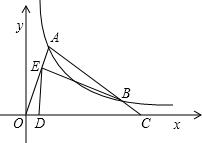 如图,在△AOC中,AC=OC,O是坐标原点,点C在x轴上,点A坐标是(1,3),则点C的坐标是________.若A点在双曲线
如图,在△AOC中,AC=OC,O是坐标原点,点C在x轴上,点A坐标是(1,3),则点C的坐标是________.若A点在双曲线 (x>0)上,AC与双曲线交于点B,点E是线段OA上一点(不与O,A重合),设点D(m,0)是x轴正半轴上的一个动点,且满足∠BED=∠AOC,当线段OA上符合条件的点E有且仅有2个时,m的取值范围是________.
(x>0)上,AC与双曲线交于点B,点E是线段OA上一点(不与O,A重合),设点D(m,0)是x轴正半轴上的一个动点,且满足∠BED=∠AOC,当线段OA上符合条件的点E有且仅有2个时,m的取值范围是________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com