练习册

  • 练习册
  • 试题
    求证:顺次连结等腰梯形各边中点所构成的四边形是菱形. 【查看更多】

     

    题目列表(包括答案和解析)

    (1)顺次连结等腰梯形的四条边的中点所得到的图形是什么样的图形?并证明你的结论.(要求:画出图形,写出已知、求证和证明)

    (2)如果把(1)中的“等腰梯形”换成另外的四边形,其他条件不变仍得同样的结论.能得出上述结论的这类四边形具备怎样的共同特征?请把此特征写出来(不需证明).

     

    查看答案和解析>>

    顺次连结等腰梯形各边中点得到一个四边形，再顺次连结所得四边形的中点得到的图形是（　　）

    查看答案和解析>>

    下列命题中，假命题是（　　）
    A、正多边形都是轴对称图形B、顺次连结等腰梯形的四边中点，所得的四边形是菱形C、在半径为6的⊙O中，长度为6的弦所对的圆周角为30°D、若⊙O1和⊙O2相交，两圆的圆心距为7cm，⊙O1的半径为3cm，则⊙O2的半径r的取值范围是4cm＜r＜10cm

    查看答案和解析>>

    顺次连结等腰梯形四边中点所得到的四边形的形状是（　　）

    查看答案和解析>>

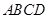    顺次连结等腰梯形各边中点，所得的四边形一定是（  ）
    A．等腰梯形B．菱形C．矩形D．平行四边形

    查看答案和解析>>


    同步练习册答案