
题目列表(包括答案和解析)
如图,各边都相等的五边形ABCDE中,∠ABC=2∠DBE,那么∠ABC为[方法提示:利用特殊值法求解.]
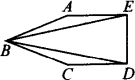
A.60°
B.120°
C.90°
D.45°
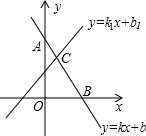 在数学学习中,及时对知识进行归纳和整理是改善学习的重要方法.善于学习的小明在学习了一次方程(组)、一元一次不等式和一次函数后,把相关知识归纳整理如下:
在数学学习中,及时对知识进行归纳和整理是改善学习的重要方法.善于学习的小明在学习了一次方程(组)、一元一次不等式和一次函数后,把相关知识归纳整理如下:| (1)一次函数的解析式就是一个二元一次方程; (2)点B的横坐标是方程①的解; (3)点C的坐标(x,y)中的x,y的值是方程组②的解.一次函数与不等式的关系;
|