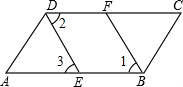已知，如图，∠ABC=∠ADC，BF、DE分别平分∠ABC与∠ADC，且∠1=∠3．求证：AB∥DC．
请根据条件进行推理，得出结论，并在括号内注明理由．
证明：∵BF、DE分别平分∠ABC与∠ADC，
∴∠1=∠ABC，∠2=．（________）
∵∠ABC=∠ADC，
∵∠________=∠________．
∵∠1=∠3，
∴∠2=________．（等量代换）
∴________∥________．（________）

已知，如图，∠ABC＝∠ADC，BF、DE分别平分∠ABC与∠ADC，且∠1＝∠3．求证：AB∥DC．请根据条件进行推理，得出结论，并在括号内注明理由．

证明：∵BF、DE分别平分∠ABC与∠ADC，

∴∠1＝∠ABC，∠2＝∠ADC．(________)

∵∠ABC＝∠ADC，

∵∠________＝∠________．

∵∠1＝∠3，

∴∠2＝________．(等量代换)

∴________∥________．(________)

在2004年雅典奥运会上，中国射击选手在逆境中顽强拼搏，终于拿下第一枚金牌．下面我们也来一个射击比赛问题．某射击运动员在一次比赛中前6次射击共中52环，如果他要打破89环(共10次射击)的记录，请你根据下列假设进行分析．

(1)如果第7次中10环，最后三次平均每次至少要中几环才能破记录？

(2)如果接着第8次只中了9环，还有破记录的希望吗？写出可能的情况．