
题目列表(包括答案和解析)
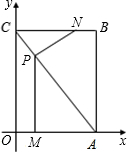
 (2010•李沧区二模)如图,四边形OABC为直角梯形,OA⊥CO,CB∥OA,OA=CO=4,BC=3.点M从O出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AO于点P,连接AC交NP于Q,连接MQ、BQ.
(2010•李沧区二模)如图,四边形OABC为直角梯形,OA⊥CO,CB∥OA,OA=CO=4,BC=3.点M从O出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AO于点P,连接AC交NP于Q,连接MQ、BQ.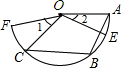 如图,四边形OABC为菱形,点B、C在以点O为圆心的
如图,四边形OABC为菱形,点B、C在以点O为圆心的 |
| EF |
 |
| EF |
 连接NP.
连接NP. 加试题:
加试题: 如图,四边形OABC为菱形,点A、B在以O为圆心的
如图,四边形OABC为菱形,点A、B在以O为圆心的 |
| DE |
| π |
| 3 |
| π |
| 3 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com