
题目列表(包括答案和解析)
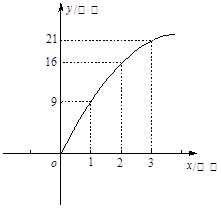
某公司推出一款新型手机,投放市场以来前3个月的利润情况如图所示,该图可以近似看作抛物线的一部分.请结合图象,解答以下问题:
【小题1】(1)求该抛物线对应的二次函数解析式;
【小题2】(2)该公司在经营此款手机过程中,第几月的利润能达到24万元?
【小题3】(3)若照此经营下去,请你结合所学的知识,对公司在此款手机的经营状况(是否亏损?何时亏损?)作预测分析.
 某公司推出一款新型手机,投放市场以来前3个月的利润情况如图所示,该图可以近似看作抛物线的一部分.请结合图象,解答以下问题:
某公司推出一款新型手机,投放市场以来前3个月的利润情况如图所示,该图可以近似看作抛物线的一部分.请结合图象,解答以下问题: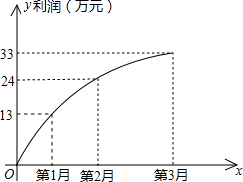 线的一部分,请结合下面的图象解答以下问题:
线的一部分,请结合下面的图象解答以下问题:湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com