
题目列表(包括答案和解析)
 要求解):①自行车行驶在摩托车前面;②自行车与摩托车相遇;③自行车行驶在摩托车后面.
要求解):①自行车行驶在摩托车前面;②自行车与摩托车相遇;③自行车行驶在摩托车后面. 26、如图表示一骑自行车者和一骑摩托车者沿相同路线由甲地到乙地行驶过程的函数图象(分别为正比例函数和一次函数).两地间的距离是80千米.请你根据图象回答或解决下面的问题:
26、如图表示一骑自行车者和一骑摩托车者沿相同路线由甲地到乙地行驶过程的函数图象(分别为正比例函数和一次函数).两地间的距离是80千米.请你根据图象回答或解决下面的问题: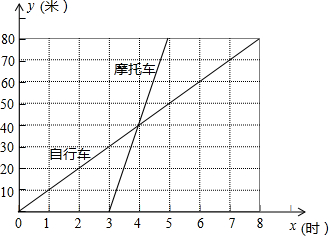 两地间的距离是80千米.请你根据图象回答或解决下面的问题:
两地间的距离是80千米.请你根据图象回答或解决下面的问题: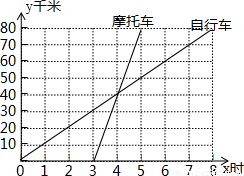
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com