
题目列表(包括答案和解析)
解:(1)OA=1,OC=2
则A点坐标为(0,1),C点坐标为(2,0)
设直线AC的解析式为y=kx+b
![]()
解得
![]() 直线AC的解析式为
直线AC的解析式为![]() ··················· 2分
··················· 2分
(2)![]() 或
或![]()
(正确一个得2分)························· 8分
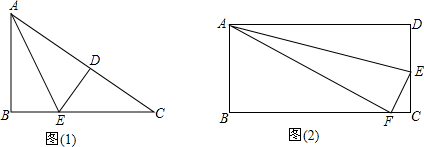
 (3)如图,设
(3)如图,设![]()
过![]() 点作
点作![]() 于F
于F
![]()
由折叠知![]()
![]()
![]() 或2··········· 10分
或2··········· 10分
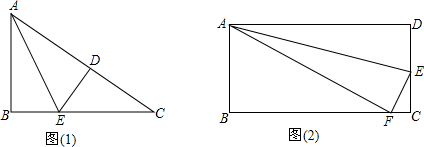

已知,AB=AD,∠ABC=∠ADC=90°,E是AC上任意一点,求证:BE=DE.
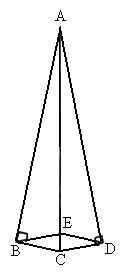
(1)分析:要证BE=DE,可证△ABC≌△BAD.由已知AB=AD,AE=AE,要证△ABE≌△ADE.只需证________=___________为此,可证________≌_________.
(2)证明:在Rt△ABC和Rt△ADC中,
∴Rt△ABC≌Rt△ADC( ),
∴∠BAE=∠DAE( ).
在△ABE和△ADE中,
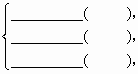
∴Rt△ABE≌Rt△ADE( ),
∴BE=DE( ).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com